страница - 101
3)получением снимков с использованием 35-миллиметровой или более узкой копировальной пленки, (такая пленка не позволяет передавать достаточно широкий диапазон плотностей оригинала);
4)путем рентгенографирования снимка-оригинала с использованием рентгеновского излучения очень низкой энергии (10... 15 кэВ). Этот способ эффективен при плотности снимка-оригинала более 4;
5)с использованием цифровой телевизионной системы или линейной матрицы детекторов (могут быть оцифрованы пленки в диапазоне плотностей почернения 1 ... 4,8); цифровое изображение может обрабатываться и запоминаться; так, оптический диск с двумя гигабайтами данных может храниться без потерь информации в течение 30 лет.
Глава 3.5
АКУСТИЧЕСКИЕ МЕТОДЫ КОНТРОЛЯ
3.5.1. ОБЩИЕ СВЕДЕНИЯ
Акустическими методами называют методы, основанные на использовании упругих колебаний и волн любых частот. Методы, использующие частоты от 20 кГц до 100 Мгц, называют ультразвуковыми.
Упругая волна представляет собой процесс распространения возмущений в среде в результате действия механических сил, происходящий благодаря упругому взаимодействию частиц среды.
Отклонение частицы от положения равновесия называется смещением величина v = = d/dt- колебательной скоростью. Колебания частиц обусловлены звуковым давлением р, представляющим собой разность между мгновенным ра и статическим ро давлениями в данной точке среды:
Р =Ра ~ Р0> Важным параметром среды является ее характеристический импеданс или удельное волновое сопротивление. Он определяется как отношение комплексных амплитуд звукового давления р к колебательной скорости v в гармонической бегущей волне: Z=i>/v,
обычно выражается произведением плотности
р среды на скорость распространения волны: Z = рс.
Для сред с небольшими потерями z можно считать действительной величиной.
Акустическим импедансом Za называют отношение комплексных амплитуд р и v в любой гармонической волне:
Za = Ph • В общем случае Za - комплексная величина.
В неразрушающем контроле встречается также понятие механического импеданса, под которым понимают отношение комплексных амплитуд гармонической возмущающей силы F и вызываемой ею колебательной скорости v в направлении силы:
Z=F/v.
В отличие от рс, характеризующего среду, механический импеданс является параметром конструкции.
Энергетической характеристикой упругой волны служит интенсивность. Для бегущей гармонической волны интенсивность
j = рсу2т /2 = р2т/ 2рс,
где vw и рт - амплитуды колебательной скорости и звукового давления соответственно.
Единицы измерения рассмотренных величин в системе СИ: смещения - м, колебательной скорости - м/с, звукового давления -Па, интенсивности - Вт/м2, характеристического и акустического импедансов - Пас/м, механического импеданса - Н-с/м.
В жидкостях и газах распространяются лишь продольные волны. В безграничных твердых телах могут существовать только продольные и поперечные (сдвиговые) волны. В продольных волнах направление колебательного движения частиц среды совпадает (или противоположно) с направлением распространения волны, в поперечных - перпендикулярно этому направлению.
В ограниченных твердых телах могут распространяться также волны других типов. Из них основное значение имеют: поверхностные волны (волны Рэлея), нормальные волны в слоях (волны Лэмба), изгибные волны, нормальные стержневые волны (волны Похгамме-ра).
Поверхностные волны распространяются по свободным поверхностям твердых тел в слое толщиной порядка длины волны. Частицы среды движутся по эллиптическим траекториям.
Волны Лэмба возбуждаются в слоях - листах, стенках труб и т.п. - и имеют волноводный механизм распространения. Скорость распространения этих волн зависит от толщины слоя и частоты. Симметричные s и антисимметричные а моды волн отличаются симметричным и антисимметричным движениями относительно среднего сечения слоя (рис. 3.5.1). Различные моды волн распространяются с разными скоростями. Изгибные волны есть частный случай антисимметричных волн Лэмба нулевого порядка Дп> когда длина волны намного больше толщины слоя.
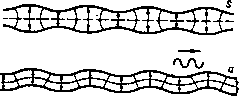
Рис. 3.5.1. Деформация пластины при распространении симметричных и антисимметричных волн
Стержневые волны во многом сходны с волнами Лэмба. Они также делятся на симметричные и антисимметричные и имеют множество мод.
Скорости продольных, поперечных и поверхностных волн в большинстве материалов не зависят от частоты. Скорости волн в пластинах и стержнях зависят от произведения толщины изделия на частоту. Это явление называют дисперсией скорости.
Скорости распространения волн всех типов определяются плотностью р среды и ее упругими составляющими. Формулы для скоростей распространения основных типов волн приведены в табл. 3.5.1, акустические свойства различных сред - в табл. 3.5.2.
При распространении в средах упругие волны ослабляются вследствие расхождения энергии в пространстве и затухания, в среде. В ультразвуковой дефектоскопии применяют высокие частоты if > 0,5 Мгц), когда отношение поперечного размера 2а преобразователя больше дины волны (2а > X, где X - длина волны).
В этом случае излучение характеризуется направленностью, т.е. основная энергия сосредоточена в пределах относительно узкого пучка. Акустическое поле излучателя обладает ближней и дальней зонами. Для круглого преобразователя радиусом а границей ближней зоны является расстояние r§ = а2 / X. В ближней зоне (г < /fc) звуковое давление меняется немонотонно, в дальней зоне - монотонно убывает. На расстояниях г » г§ зависимость звукового давления от угла 0 с осью излучения представляется диаграммой направленности (рис. 3.5.2), имеющей основной и несколько боковых лепестков. Угол раскрытия основного лепестка этой диаграммы
А
в = arcsin0,67 —.
/ а
Направленность при приеме аналогична направленности при излучении.
ю s* о s* ю
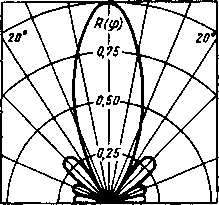
Рис. 3.5.2. Диаграмма направленности поля излучения дискообразного преобразователя с 2а/Х — 5 в полярных координатах
При распространении сферической акустической волны в безграничной среде ослабление звукового давления происходит по закону
г
Здесь член 1/г2 характеризует ослабление
-Sr
вследствие расхождения, множитель е вследствие затухания.
Коэффициент затухания 5 = — lnjр / р
г
выражается в Неперах/м (Нп/м) и имеет размерность м1. Часто его представляют также в децибелах / м (дБ/м). При этом 1 Нп/м = = 8,686 дБ/м, 1 дБ/м=0,1151 Нп/м.
Коэффициент затухания складывается из коэффициентов поглощения и рассеяния:
5 = 5л + 8р.
При поглощении звуковая энергия переходит в тепловую, а при рассеянии остается звуковой, но уходит из направленно распространяющейся волны в результате отражений от неоднородностей среды.
В газах и жидкостях, не засоренных взвешенными частицами, пузырьками воздуха (в жидкости), рассеяние отсутствует и затухание определяется только поглощением. Коэффициент поглощения пропорционален квадрату частоты.
Для твердых тел коэффициент поглощения чаще всего пропорционален частоте. Для
5п
стали-=0,1 ч- 1,5 Нп/МГцм; для алюминия
/
0,05 + 0,06; для магния 0,1. Поглощение опре-
3.5.1. Типы волн
Среда распространения | Тип (название) волны | Характеристика волны | Скорость распространения | |
Жидкость ИЛИ газ | Продольные (растяжения-сжатия) | Периодические расширения и сжатия среды | ||
Безграничное твердое тело | Продольные (растяжения-сжатия, безвихревые) | Частицы колеблются в направлении распространения волны | 1 *(l-v) \p(l+v)(l-2v) | |
Поперечные (сдвига, эквиволюминальные) | Частицы колеблются в плоскости, перпендикулярной направлению распространения волны | \ E = - * 0,55c, V2p(l+v) | ||
Поверхность полубезграничного тела | Поверхностные (Рэлея) | Волна распространяется по поверхности тела | cs = | 0,87 + l,12v -С, «0,93с, 1 + v |
Бесконечная пластина толщиной h | Изгибная | Изгиб пластины со сдвигом | cb (* | = Jvih • J--- ,I2p(l-v) » h) |
Нормальная симметричная (мода .So волны Лэмба) | Продольные колебания с изменением поперечных размеров | -\) (X » h) | ||
Бесконечный стержень диаметром d | Продольные (растяжения-сжатия) | Продольные колебания с изменением поперечных размеров | (X » d) | |
Примечание. Здесь К - модуль всестороннего сжатия; Е - модуль упругости;
v - коэффициент Пуассона; со - угловая частота; р - плотность; X - длина волны.
содержание:
[стр.Введение] [стр.1] [стр.2] [стр.3] [стр.4] [стр.5] [стр.6] [стр.7] [стр.8] [стр.9] [стр.10] [стр.11] [стр.12] [стр.13] [стр.14] [стр.15] [стр.16] [стр.17] [стр.18] [стр.19] [стр.20] [стр.21] [стр.22] [стр.23] [стр.24] [стр.25] [стр.26] [стр.27] [стр.28] [стр.29] [стр.30] [стр.31] [стр.32] [стр.33] [стр.34] [стр.35] [стр.36] [стр.37] [стр.38] [стр.39] [стр.40] [стр.41] [стр.42] [стр.43] [стр.44] [стр.45] [стр.46] [стр.47] [стр.48] [стр.49] [стр.50] [стр.51] [стр.52] [стр.53] [стр.54] [стр.55] [стр.56] [стр.57] [стр.58] [стр.59] [стр.60] [стр.61] [стр.62] [стр.63] [стр.64] [стр.65] [стр.66] [стр.67] [стр.68] [стр.69] [стр.70] [стр.71] [стр.72] [стр.73] [стр.74] [стр.75] [стр.76] [стр.77] [стр.78] [стр.79] [стр.80] [стр.81] [стр.82] [стр.83] [стр.84] [стр.85] [стр.86] [стр.87] [стр.88] [стр.89] [стр.90] [стр.91] [стр.92] [стр.93] [стр.94] [стр.95] [стр.96] [стр.97] [стр.98] [стр.99] [стр.100] [стр.101] [стр.102] [стр.103] [стр.104] [стр.105] [стр.106] [стр.107] [стр.108] [стр.109] [стр.110] [стр.111] [стр.112] [стр.113] [стр.114] [стр.115] [стр.116] [стр.117] [стр.118] [стр.119] [стр.120] [стр.121] [стр.122] [стр.123] [стр.124] [стр.125] [стр.126] [стр.127] [стр.128] [стр.129] [стр.130] [стр.131] [стр.132] [стр.133] [стр.134] [стр.135] [стр.136] [стр.137] [стр.138] [стр.139] [стр.140] [стр.141] [стр.142] [стр.143] [стр.144] [стр.145] [стр.146] [стр.147] [стр.148] [стр.149] [стр.150] [стр.151]
