страница - 102
3.5.2. Акустические свойства различных сред
Вещество | Плотность Р, 103 кг/м3 | Скорость распространения волн с, 103 м/с | Характеристиче -ский импеданс для продольных волн, МПас/м | ||
продольных | поперечных | поверхностных | |||
Металлы и сплавы | |||||
Алюминий | 2,7 | 6,36 | 3,13 | 2,9 | 17,2 |
Бронза | 8,5 - 8,9 | 3,5 - 3,8 | 2,3 - 2,5 | 2,1-2,3 | 30 - 34 |
Вольфрам | 19,25 | 5,32 | 2,7 | 2,65 | 102,7 |
Дюралюминий | 2,7 - 2,8 | 6,25-6,35 | 3,0 - 3,2 | 2,8 - 3,0 | 17,2-20,0 |
Железо | 7,8 | 5,91 | 3,23 | 3,0 | 46,3 |
Латунь | 8,5 | 4,43 | 2,12 | 1,95 | 37,7 |
Магний | 1,74 | 5,77 | 3,05 | 2,875 | 10,1 |
Медь | 8,9 | 4,72 | 2,44 | 2,26 | 42,0 |
Молибден | 10,09 | 6,29 | 3,35 | з,п | 63,5 |
Никель | 8,8 | 5,63 | 2,96 | 2,64 | 49,5 |
Олово | 7,3 | 3,32 | 1,67, | 1,56 | 24,2 |
Ртуть | 13,6 | 1,45 | - | - | 19,8 |
Свинец | 11,4 | 2,16 | 0,85 | 0,79 | 24,6 |
Серебро | 10,5 | 3,60 | 1,59 | 1,48 | 38,0 |
Сталь: | |||||
коррозионностойкая | 8,03 | 5,66-6,14 | 3,12-3,25 | 3,1 | 45,5-49,3 |
углеродистая | 7,8 | 5,90-5,94 | 3,22-3,25 | 3,0 | 46,2- 46,4 |
Титан | 4,5 | 6,10 | 3,13 | 2,91 | 27,5 |
Цинк | 7,1 | 4,17 | 2,41 | 2,22 | 29,6 |
Чугун | 7,2 | 3,5 - 5,6 | 2,2 - 3,2 | - | 25 - 40 |
Неметаллы | |||||
Бетон | 1,8 - 2,8 | 2,1 - 5,2 | - | - | 4 - 14,5 |
Капрон | 1,1 | 2,64 | - | - | 2,9 |
Кварц плавленный | 2,2 | 5,93 | 3,75 | 3,39 | 13,0 |
Нейлон, перлон | 1,1 - 1,2 | 1,8 - 2,2 | - | - | 1,8 - 2,7 |
Стекло органическое | 1,18 | 2,65-2,75 | 1,12-1,13 | 1,05 | 3,0 - 3,2 |
Окись алюминия | 3,7 - 3,9 | 10 | - | - | 37 - 39 |
(корунд) | |||||
Полистирол | 1Д | 2,37 | 1,12 | 1,04 | 3,0 |
Резина: | |||||
сырая | 1,3 - 2,1 | 1,48 | - | - | 1,9 - 3,1 |
вулканизированная | 0,9 - 1,6 | 1,5 - 2,3 | - | - | 1,3 - 3,7 |
Смола акриловая | 1,18 | 2,67 | 1,12 | - | 3,2 |
Стекло оконное | 2,6 | 5,7 | 3,4 | 3,1 | 14,5 |
Текстолит | 1,2 - 1,3 | 2,63 | - |
| 3,1 - 3,9 |
Фторопласт | 2,2 | 1,35 | - | - | 3 |
Фарфор | 2,4 | 5,3 - 5,35 | 3,5 - 3,7 | 1,3 - 1,4 | |
Эбонит | 1,2 | 2,4 |
|
| 2,9 |
Эпоксидная смола | 1,15- 1,3 | 2,5 - 2,8 | - | 2,8 - 3,7 | |
твердая | |||||
Жидкости (20° С) | |||||
Вода | 0,998 | 1,490 |
| 1,49 | |
Глицерин | 1,265 | 1,923 |
|
| 2,42 |
Керосин | 0,825 | 1,295 |
|
| 1,45 |
Масло: | |||||
машинное (автол) | 0,89- 0,96 | 1,74 |
| 1,5 - 1,7 | |
трансформаторное | 0,9 - 0,92 | 1,38-1,40 |
|
| 1,25-1,27 |
Спирт этиловый | 0,789 | 1,180 | - | - | 0,93 |
Газы (0° С) | |||||
Водород | 0,9-Ю4 | 1,248 |
|
| 1Д10-4 |
Воздух | 1,3-10-3 | 0,331 | - | - | 4,310"4 |
деляет затухание акустических волн в аморфных твердых телах, а также в монокристаллах.
Большинство твердых тел состоит из большого числа зерен-кристаллитов, на границах которых происходит рассеяние ультразвуковых волн. Вследствие этого роль рассеяния оказывается значительной и часто превалирующей. Особенно велико рассеяние в материалах, состоящих из разнородных частиц (бетон, гранит, чугун), и в материалах с большой упругой анизотропией - разной скоростью упругих волн для разных направлений в кристалле (медь, аустенитная сталь).
Для металлов 5р увеличивается с ростом упругой анизотропии, среднего размера кристаллитов D и частоты:
В области
ГЛ.Г 2
> » Df , а при X > 10 D „
~f" (п =2-4). X/D =4+10 5
л3 И
К примеру, для продольных
X>10D\
в малоуглеродистой стали и поперечных волн при
57 * 0,12/+20Z>3/\
5, « 0,1/ +105Z)3/4.
Здесь D - в мм,/- в МГц, 5 - в Нп/м.
Значения коэффициентов затухания в зависимости от частоты для некоторых сталей приведены на рис. 3.5.3.
0,3.
0,05
0,03 OfiA
W f qoi
ft | |||||||||
ft | /7 | ||||||||
/ | 7 | ||||||||
/ | t | ||||||||
/ / | / | m | 4 | ||||||
/V | V | ||||||||
/ | // | ||||||||
I . | 7 | oo | |||||||
. | -1 | ||||||||
0 4 4 6 в Ю 12 f4 16 iMPu
Рис. 3.5.3. Коэффициент затухания продольных волн в сталях
(даны марка стали и средний размер зерна в мм)
В пластиках значения коэффициентов затухания обычно больше, чем в металлах, и определяются они в основном поглощением (рис. 3.5.4). Минимальный размер дефекта, выявляемого методом отражения, ограничен дифракцией упругих волн.
0}
ог
Qf
05 /,МГц 10
Рис. 3.5.4. Коэффициент затухания продольных волн в
/ - фторопласт; 2 - отвержденная эпоксидная смола ЭД-5; 3 - эбонит; 4 - компаунд К-153; 5 - органическое стекло; 6 - полистирол
При d/X < 0,5 волна огибает дефект и отражение от него резко уменьшается. Поэтому с ростом частоты (уменьшением X) чувствительность растет. Однако увеличению частоты препятствует рост поглощения и шумов, обусловленных рассеянием волн на неодно-родностях структуры материала. В результате частоту прозвучивания выбирают путем компромисса с учетом структуры материала изделия.
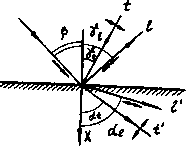
Рис. 3.5.5. Отражение, преломление и трансформации при падении продольной волны ва границу раздела двух твердых сред
Граница двух протяженных сред. Падающая на границу двух протяженных сред плоская волна частично проходит, частично отражается и может трансформироваться. В твердых телах (рис. 3.5.5) возникают две (продольная и поперечная) отраженные и две преломленные волны с направлениями по закону синусов (закону Снеллиуса):
sinp sin у/ sin у, sinctj sin а.
где Р, у и а - углы падения, отражения и преломления; с - скорости волн; индексы / и /
обозначают продольные и поперечные волны, для нижней среды индексы имеют штрих (), скорость падающей волны - без индекса. Если одна среда (или обе) жидкая или газообразная, то поперечные волны в ней не существуют и количество волн сокращается.
Амплитуды каждой отраженной или прошедшей волны определяются коэффициентами отражения или прозрачности Я или D. Эти коэффициенты могут быть по амплитудам смещения, акустического давления или других переменных величин. Часто используют коэффициенты по потокам энергии, перпендикулярным границе раздела R и D (будем называть "по энергии"). Для этих коэффициентов справедливы общие закономерности:
1)Сумма всех коэффициентов отражения и прозрачности по энергии равна 1 (закон сохранения энергии):
Ru +Rlt+Dir+Dir =1.
2)Коэффициенты отражения по амплитуде однотипной волны с двух сторон от границы равны по модулю и обратны по знаку:
Rir= -Rrr> Rtt = -Rtr
3)Коэффициент прозрачности по энергии равен произведению коэффициентов по амплитуде в двух направлениях. Например:
5,, =Dti.Da =Da.
То же относится к коэффициентам отражения разнотипных волн:
Rlt = RltRtl = tl
Эта закономерность (в части прохождения) важна для дефектоскопии, поскольку границу изделия волна проходит дважды.
На рис. 3.5.6, в и 3.5.7 показаны расчетные коэффициенты прозрачности по энергии для границ некоторых сред. Кроме того на рис. 3.5.6, д, б для границы оргстекло-сталь даны коэффициенты прозрачности по амплитуде смещения при падении продольной волны из оргстекла в сталь под углом р (а) и при падении продольной или поперечной волн из стали в оргстекло под углами а/ и at (б). На дополнительных шкалах - углы преломления. Штриховыми линиями на рис. 3.5.6, в показаны коэффициенты прозрачности по энергии при конечной толщине слоя масла 5 (указано в долях длины волны в масле).
При первом и втором критических углах
Р* = arcsin. /с), Р* = arcsinc,. /с)
преломленные волны (продольная и поперечная соответственно) превращаются в неодно-
о.г 0.1
о
(.8
1**1 ,6 1**1
t* 48
------ | J | |||||
Ь)
OA
о
0.2
о
! | М | За1 | ||||
0,07 | 1 | — | ||||
10 20 | Ю Ц0 fi.r~* so МО *t.fr**60 70 90 | |||||
Ю 20 59 ¥> 50 ТО" 10 20 ЪО | ||||||
Рис. 3.5.6. Коэффициенты прозрачности для границы оргстекло - слой масла - сталь:
по амплитуде в прямом (а), обратном (б)
направлениях и по энергии (в) (штрихпунктирная линия - эксперимент)
ЖЛ *> Я JO 1*0 SO 7990
а)
01S\
град.
в/й . град.
10 | 20 | 30 1 но | Ъ 40 | 70 90 | ||
\ | ||||||
Рис. 3.5.7. Коэффициент прозрачности по энергии для границы вода - сталь
(штрихпунктирная линия - эксперимент)
родные, т.е. соответствующая волна распространяется вдоль границы, фронт ее перпенди-
содержание:
[стр.Введение] [стр.1] [стр.2] [стр.3] [стр.4] [стр.5] [стр.6] [стр.7] [стр.8] [стр.9] [стр.10] [стр.11] [стр.12] [стр.13] [стр.14] [стр.15] [стр.16] [стр.17] [стр.18] [стр.19] [стр.20] [стр.21] [стр.22] [стр.23] [стр.24] [стр.25] [стр.26] [стр.27] [стр.28] [стр.29] [стр.30] [стр.31] [стр.32] [стр.33] [стр.34] [стр.35] [стр.36] [стр.37] [стр.38] [стр.39] [стр.40] [стр.41] [стр.42] [стр.43] [стр.44] [стр.45] [стр.46] [стр.47] [стр.48] [стр.49] [стр.50] [стр.51] [стр.52] [стр.53] [стр.54] [стр.55] [стр.56] [стр.57] [стр.58] [стр.59] [стр.60] [стр.61] [стр.62] [стр.63] [стр.64] [стр.65] [стр.66] [стр.67] [стр.68] [стр.69] [стр.70] [стр.71] [стр.72] [стр.73] [стр.74] [стр.75] [стр.76] [стр.77] [стр.78] [стр.79] [стр.80] [стр.81] [стр.82] [стр.83] [стр.84] [стр.85] [стр.86] [стр.87] [стр.88] [стр.89] [стр.90] [стр.91] [стр.92] [стр.93] [стр.94] [стр.95] [стр.96] [стр.97] [стр.98] [стр.99] [стр.100] [стр.101] [стр.102] [стр.103] [стр.104] [стр.105] [стр.106] [стр.107] [стр.108] [стр.109] [стр.110] [стр.111] [стр.112] [стр.113] [стр.114] [стр.115] [стр.116] [стр.117] [стр.118] [стр.119] [стр.120] [стр.121] [стр.122] [стр.123] [стр.124] [стр.125] [стр.126] [стр.127] [стр.128] [стр.129] [стр.130] [стр.131] [стр.132] [стр.133] [стр.134] [стр.135] [стр.136] [стр.137] [стр.138] [стр.139] [стр.140] [стр.141] [стр.142] [стр.143] [стр.144] [стр.145] [стр.146] [стр.147] [стр.148] [стр.149] [стр.150] [стр.151]
