страница - 34
ся в среде частицами, плотность которых отличается от плотности основной среды. При этом в соответствии с законом Допплера, изменяется частота отраженного сигнала. Разность частот определяется уравнением
* *COSP
ч
где fi - частота отраженного сигнала; uq - скорость звука; v - скорость потока среды; Р -угол между направлением потока и направлением распространения ультразвуковых волн.
При постоянных значениях f\, cosP и асу разность
/l-/=*0V.
Таким образом, сдвиг частот прямо пропорционален скорости потока v и может быть использован для измерения расхода без потери давления.
Ряд измерителей расхода основан на определении частоты вихрей, возникающих в потоке при помещении в него специальных устройств. Эти завихрения называются вихревой дорожкой Кармана. При числах Рейнольд-са, превышающих 70, для бесконечно длинного цилиндра диаметром d связь между частотой вихрей / и скоростью потока v определяется числом Струхаля:
C=/rf/v.
Число Струхаля остается неизменным в широком диапазоне чисел Рейнольдса, поэтому скорость потока может быть определена измерением частоты вихрей.
Иногда в контролируемом потоке создаются вращательные завихрения, перемещающиеся в направлении его движения и воспринимаемые преобразователем, конструкция которого выполнена без каких-либо подвижных частей. Вращающийся поток создается установленными на входе расходомера направляющими пластинками, вытянутыми по контуру в направлении движения потока. Встроенный в стенку расходомера терморезистор выдает импульсы, частота которых пропорциональна скорости потока, которые поступают затем в электронный блок. На выходе расходомера установлен механический струевыпря-митель, устраняющий вращение потока.
Измеритель расхода с качающимся телом пригоден для газов и жидкостей. Прибор показан на рис. 1.11.8. Через штуцер 1 контролируемая среда поступает в корпус, протекает через два прямоугольных канала 2 и, выходя из них в сечении 3, воздействует в точке 4 на качающееся призмообразное тело. Через штуцер 5 среда удаляется из прибора.
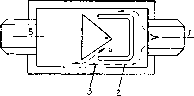
Рис. 1.11.8. Измеритель расхода с качающимся чувствительным элементом
Качание тела при движении среды возникает вследствие того, что случайные возмущения выводят язычок, находящийся в среднем положении, из состояния покоя. Возмущающие усилия возникают вследствие турбулентности потока, которая практически всегда образуется в нем. После возникновения колебаний язычка их частота при постоянной плотности среды пропорциональна расходу.
Гироскопический расходомер состоит из V-образной измерительной трубки, совершающей крутильные колебания с частотой 50 - 60 Гц относительно оси вращения. Кори-олисова сила, воздействующая на тело, движущееся с нелинейным ускорением, скручивает трубку пропорционально произведению массы на скорость. Угол скручивания определяется оптоэлектронным датчиком, по сигналу которого вычисляется массовый расход. Свойства, протекающей через прибор среды (температура, плотность или вязкость), не влияют на его показания, поэтому гироскопические расходомеры применимы для измерений двухфазных потоков (например, воды и водяного пара) и успешно используются для измерений массового расхода угольной пыли.
Лазерный метод измерения скорости потока основан на измерении времени перемещения пылевых частиц на отрезке пути, ограниченном двумя лазерными лучами. Подобный лазерный прибор используется, например, для измерения расхода в аэродинамических трубах; при этом контролируется скорость всегда присутствующих в воздухе пылевых частиц. Достоинством метода является возможность непосредственного измерения скорости без установки в трубопроводе дополнительных устройств и без каких-либо воздействий на поток. Аналогично можно измерять скорость потоков жидкостей.
При перемещении частиц относительно неподвижной точки, из которой ведется наблюдение, частота рассеиваемого пылью света изменяется пропорционально скорости частиц согласно закону Допплера. В типовом устройстве допплеровский эффект для красного изо
лучения гелий-неонового лазера (6328А) составляет около 1 МГц при скорости потока 1 м/с. Метод позволяет бесконтактно контроли-
ровать скорость потоков жидкостей и газов в диапазоне от 0,01 мм/с до 1 ООО м/с. Метод применим при достаточной прозрачности среды и незначительном содержании в ней частиц, отражающих излучение.
Глава 1.12
ОБРАБОТКА РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ
Выбор математических методов определяется поставленными задачами измерения. Фундаментальная теория измерения имеет два основных направления: физическое и математическое. Первое основано на тезисе о неизбежности погрешности измерения. Второе - на абстракции "абсолютно точного" сравнения. Поэтому математические проблемы при физических измерениях возникают в первую очередь вследствие того, что полученное при наблюдении значение величины отличается от действительного и в качестве последнего принимают какую-нибудь его оценку. Поиск приемлемой оценки приводит к различным задачам определения ее значения в зависимости от: 1) характера измеряемой величины (величина неизменяющаяся, изменяющаяся во времени или в зависимости от другой величины) и 2) особенностей процесса измерения (прямое или косвенное измерение; равноточные или неравноточные измерения; метод непосредственной оценки или сравнения).
Требования к представлению результата измерения величины независимо от особенностей процесса измерения определяют следующие необходимые задачи обработки результатов наблюдений:
определение оценки математического ожидания;
определение среднего квадратического отклонения (дисперсии);
вычисление доверительного интервала;
оценка (выявление) грубых погрешностей;
оценка и выбор закона распределения.
Иногда требуется определить медиану, моду, вариационный размах и коэффициент вариации. Кроме того, использование измерений для определения зависимостей, моделей и
характеристик процессов привело к постановке ряда типовых задач, непосредственно основанных на обработке результатов измерений.
1.12.1. ОБРАБОТКА РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ ПРИ ПРЯМЫХ ИЗМЕРЕНИЯХ
Предположим, что произведено п наблюдений Х\9 Х2, ... , хп и точность получения X/ для любого / одинакова, то есть имеют место равноточные измерения. Тогда, при нормальном законе распределения погрешностей, в качестве результата измерения принимаем среднее арифметическое значение
*=-]►>,.(1.12.1)
Для достаточно больших п *) можно ограничиться полученным результатом. Но часто при измерениях по разным соображениям п ограничено. Тогда необходимо указать доверительный интервал для х . И во всех случаях х не дает оценки точности процесса измерения.
Для оценки точности измерения или рассеяния значений физической величины используют дисперсию сг2 или среднее квадрати-ческое отклонение сг.
При ограниченном п представительную и несмещенную 2> оценку а определяют в виде
В качестве относительной характеристики рассеяния может использоваться коэффициент вариации:
V = (5/Зс)100%.
Он показывает, насколько велико рассеяние по сравнению со средним значением. И в частности, показывает долю некорректируемой погрешности измерения, если среднее значение характеризует систематическую составляющую погрешности измерения.
1Значение п можно считать достаточно большим, если при этом рассчитываемые параметры пренебрежимо мало отличаются от параметров генеральной совокупности объема N » п. В частности, х и S пренебрежимо мало отличаются от математического ожидания и а. Например, п можно считать достаточно большим, если доверительный интервал на порядок меньше допускаемой погрешности измерения.
2Понятия несмещенной, эффективной и состоятельной оценки параметров генеральной совокупности используются в следующем смысле: несмещенная - оценка, математическое ожидание которой совпадает с оцениваемым параметром при любом объеме выборки; эффективная - оценка, имеющая минимально возможную дисперсию; состоятельная - оценка, сходящаяся по вероятности к тому или иному параметру закона распределения.
1.12.1. Нормированная функция Лапласа Фо(?)
Z | Сотые доли для Z | |||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
0,0 | 0,0000 | 040 | 080 | 120 | 160 | 199 | 239 | 279 | 319 | 359 |
0,1 | 398 | 438 | 478 | 517 | 557 | 596 | 636 | 675 | 714 | 753 |
0,2 | 793 0,1... | 832 | 871 | 910 | 948 | 987 | 026 | 064 | 103 | 141 |
0,3 | 179 | 217 | 255 | 293 | 331 | 368 | 406 | 443 | 480 | 517 |
0,4 | 554 | 591 | 628 | 664 | 700 | 736 | 772 | 808 | 884 | 879 |
0,5 | 915 | 950 | 985 | |||||||
0,2... | 019 | 054 | 088 | 123 | 157 | 190 | 224 | |||
0,6 | 257 | 291 | 324 | 357 | 389 | 422 | 454 | 486 | 517 | 549 |
0,7 | 580 | 611 | 642 | 673 | 703 | 734 | 764 | 794 | 823 | 852 |
0,8 | 881 | 910 | 939 | 967 | 995 | |||||
0,3... | 023 | 051 | 078 | 106 | 133 | |||||
0,9 | 159 | 186 | 212 | 238 | 264 | 289 | 315 | 340 | 365 | 389 |
1,0 | 413 | 437 | 461 | 485 | 508 | 583 | 554 | 577 | 599 | 621 |
1,1 | 643 | 665 | 686 | 708 | 729 | 749 | 770 | 790 | 810 | 830 |
1,2 | 849 0,4... | 869 | 888 | 907 | 925 | 944 | 962 | 980 | 997 | 015 |
1,3 | 032 | 049 | 066 | 082 | 099 | 115 | 131 | 147 | 162 | 177 |
1,4 | 192 | 207 | 222 | 236 | 251 | 265 | 279 | 292 | 306 | 319 |
1,5 | 332 | 345 | 357 | 370 | 382 | 394 | 406 | 418 | 429 | 441 |
1,6 | 452 | 463 | 474 | 484 | 495 | 505 | 515 | 525 | 535 | 545 |
1,7 | 554 | 564 | 573 | 582 | 591 | 599 | 608 | 616 | 625 | 633 |
1,8 | 641 | 649 | 656 | 664 | 671 | 678 | 686 | 693 | 699 | 706 |
1,9 | 713 | 719 | 726 | 732 | 738 | 744 | 750 | 756 | 761 | 767 |
2,0 | 772 | 778 | 783 | 788 | 793 | 798 | 803 | 808 | 812 | 817 |
2,1 | 821 | 826 | 830 | 834 | 838 | 842 | 846 | 850 | 854 | 857 |
2,2 | 860 | 864 | 867 | 871 | 874 | 877 | 880 | 883 | 886 | 889 |
966 | 474 | 906 | 263 | 545 | 755 | 894 | 962 | 962 | 893 | |
2,3 | 892 | 895 | 898 | 900 | 903 | 906 | 908 | 911 | 913 | 915 |
759 | 559 | 296 | 969 | 581 | 133 | 625 | 060 | 437 | 758 | |
2,4 | 918 | 920 | 922 | 924 | 926 | 928 | 930 | 932 | 934 | 936 |
025 | 237 | 397 | 506 | 564 | 572 | 531 | 493 | 309 | 128 | |
2,5 | 937 | 939 | 941 | 942 | 944 | 946 | 947 | 949 | 950 | 952 |
903 | 634 | 323 | 969 | 574 | 139 | 664 | 151 | 600 | 012 | |
2,6 | 953 | 954 | 956 | $57 | 958 | 959 | 960 | 962 | 963 | 964 |
388 | 729 | 035 | 308 | 547 | 754 | 930 | 074 | 169 | 274 | |
2,7 | 0,4965 | 966 | 967 | 968 | 969 | 970 | 971 | 971 | 972 | 973 |
330 | 358 | 359 | 333 | 280 | 202 | 099 | 972 | 621 | 646 | |
содержание:
[стр.Введение] [стр.1] [стр.2] [стр.3] [стр.4] [стр.5] [стр.6] [стр.7] [стр.8] [стр.9] [стр.10] [стр.11] [стр.12] [стр.13] [стр.14] [стр.15] [стр.16] [стр.17] [стр.18] [стр.19] [стр.20] [стр.21] [стр.22] [стр.23] [стр.24] [стр.25] [стр.26] [стр.27] [стр.28] [стр.29] [стр.30] [стр.31] [стр.32] [стр.33] [стр.34] [стр.35] [стр.36] [стр.37] [стр.38] [стр.39] [стр.40] [стр.41] [стр.42] [стр.43] [стр.44] [стр.45] [стр.46] [стр.47] [стр.48] [стр.49] [стр.50] [стр.51] [стр.52] [стр.53] [стр.54] [стр.55] [стр.56] [стр.57] [стр.58] [стр.59] [стр.60] [стр.61] [стр.62] [стр.63] [стр.64] [стр.65] [стр.66] [стр.67] [стр.68] [стр.69] [стр.70] [стр.71] [стр.72] [стр.73] [стр.74] [стр.75] [стр.76] [стр.77] [стр.78] [стр.79] [стр.80] [стр.81] [стр.82] [стр.83] [стр.84] [стр.85] [стр.86] [стр.87] [стр.88] [стр.89] [стр.90] [стр.91] [стр.92] [стр.93] [стр.94] [стр.95] [стр.96] [стр.97] [стр.98] [стр.99] [стр.100] [стр.101] [стр.102] [стр.103] [стр.104] [стр.105] [стр.106] [стр.107] [стр.108] [стр.109] [стр.110] [стр.111] [стр.112] [стр.113] [стр.114] [стр.115] [стр.116] [стр.117] [стр.118] [стр.119] [стр.120] [стр.121] [стр.122] [стр.123] [стр.124] [стр.125] [стр.126] [стр.127] [стр.128] [стр.129] [стр.130] [стр.131] [стр.132] [стр.133] [стр.134] [стр.135] [стр.136] [стр.137] [стр.138] [стр.139] [стр.140] [стр.141] [стр.142] [стр.143] [стр.144] [стр.145] [стр.146] [стр.147] [стр.148] [стр.149] [стр.150] [стр.151]
