страница - 39
Статистическую оценку автокорреляционной функции находят по формуле
п-» 1-1
где х - среднее значение х(, взятых внутри выбранного отрезка случайной функции.
Оценка нормированной автокорреляционной функции:
-*)(*/4Ц ~Х)
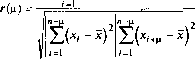
Оценка взаимной корреляционной функции двух стационарных случайных процессов:
1.12.7. ОБРАБОТКА ДАННЫХ ПРИ ИЗМЕРЕНИИ КАЧЕСТВА
Особенности измерения качества связаны, в первую очередь, с тем, что по определению качество - это совокупность свойств, что обусловливает два этапа решения задачи количественной оценки качества: измерение отдельных свойств (характеристик или показателей); получение совокупного значения количественной оценки качества. В общем случае совокупность свойств (характеристик или показателей) целесообразно разделить на две группы: свойства, полностью определяющиеся величинами, которые выражаются в единицах, имеющих эталоны; свойства, которые не определяются в единицах, имеющих эталоны. Последние можно разделить на свойства (характеристики или показатели), количественные значения которых вычисляются по соотношениям следующим из определения, и на свойства (характеристики или показатели), количественная оценка которых требует создания специальных шкал, что приводит к специфическим задачам обработки данных, полученных при измерении этих свойств. Основным методом количественной оценки последней группы свойств является экспертный метод, в основе которого лежит присвоение экспертом каждому свойству (характеристике или процессу) численного значения по выбранной шкале.
Экспертным методом решаются следующие типовые задачи:
-сравнение двух и более номинально одинаковых изделий (процессов);
-сравнение изделий или процессов одинакового функционального назначения;
-ранжирование характеристик изделия (или процесса) или ранжирование изделий (или процессов).
Для обеспечения качества измерения экспертным методом привлекается группа экспертов и поэтому задача обработки данных разделяется на две, имеющие самостоятельное значение. Обработка данных, полученных от каждого эксперта и объединение результатов оценки всех экспертов с учетом их компетентности.
Обработка данных одного эксперта. При
формализации перечисленных задач можно свести их к одной задаче, которую рассмотрим на примере ранжирования свойств (характеристик или показателей).
Предположим, что качество изделия (или процесса) описывается п показателями, которые не выражаются через величины, имеющие эталоны единиц, и требуют создания специальных шкал для их количественной оценки. На первом этапе поставим задачу разделить показатели по их значимости, используя количественные соотношения значимостей.
Одним из эффективных методов экспертной оценки является метод парных сравнений. При этом эксперт по выбранной шкале дает количественную оценку сравнения у-го показателя с к-м. Обозначим значение этой оценки- Яд. В этом случае рекомендуется использовать шкалу, построенную по следующему правилу:
1, если j-й и к-й показатели имеют одинаковую важность; 3, если j -й показатель немного важнее к -го;
-< 5, если j -й показатель существенно
важнее к -го;
7, если j -й показатель значительно важнее к -го;
9, если j -й показатель абсолютно важнее к -го.
/, j = 1, ... , т, где т - число характеристик. В общем случае п ф т, но это усложняет расчеты. Эксперт может назначить и промежуточные значения Яд, то есть 2, 4, 6 или 8.
На а у накладываются следующие условия:
1)ay — 1 при / =у;
2)ау > О, / =1, ... , п\
3)atj = 1 / aJh ij= 1, ... , п.
(1.12.6)
Если эксперт был последовательным в назначении оценок, то они будут удовлетворять условию
aij ajk = aik-После назначения для каждого /-го эксперта составляется матрица парных значений:
11 "12
21 "22
л1п
... а
2п
лп\ ип2 ••• ~пп где п - число экспертов и число показателей качества, оцениваемых каждым экспертом.
Примем, что при ранжировании каждому /-му показателю необходимо поставить в соответствие некоторое положительное число Wt (/=1, ... , /я), такое, что
т
Q<Wt< \ и Yji =L ы\
Wi назовем коэффициентом относительной важности /-го показателя качества. Очевидно, что, придавая Wt другой смысл, будет решаться другая задача. Совокупность Wi для каждого /-го эксперта образует вектор-столбец:
Элементы Яд матриц парных сравнений являются оценками отношений элементов Wj и Wk вектора-столбца.
Если условие (1.12.6) выполняется, то обеспечивается равенство
AW = m-W.
Тогда для оценки коэффициентов относительной важности можно использовать формулу: Щ = 1 / а/а, i = 1, ... , /я.
(к - номер любой строки).
Если условие (1.12.6) не выполняется, для определения Щ используется уравнение
где А.тах - максимальное собственное значение матрицы А.
При решении уравнения последовательно находят А.тах и соответствующий этому
значению собственный вектор W. Для удобства сопоставления и для дальнейших расчетов Wf нормируют по формуле
/=1
В качестве характеристики согласованности суждений каждого эксперта по методике Саати используется коэффициент согласованности
C/ = (Xm>x-m
Полагая, что рассогласованность увеличивает меру случайного, для матриц различной размерности установлены следующие значения случайного индекса RI:
Размерность матрицы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
RI | 0 | 0 | 0,58 | 0,9 | 1,12 | 1,24 | 1,32 | 1,41 | 1,45 | 1,49 |
Для оценки экспертов используют отношение соответствия
CR = CI / RI. Если CR < 0,1, то оценки экспертов можно считать не случайными и матрицу парных сравнений можно использовать без уточнений.
Объединение оценок группы экспертов может проводиться различными методами. Один из наиболее простых состоит в том, что элементы матрицы А вычисляются как средне-квадратические значения:
Недостаток метода в том, что слабо учитывается различие в компетентности экспертов.
Другой метод основан на использовании Хтах как характеристики несогласованности оценок экспертов. Здесь используются оценки коэффициентов CI в виде
С1 ~ Zrnax Amax > 1 ~ V/-1 )/ Эти оценки нормируют по формуле
/ /=1
Элементы общей матрицы 4 вычисляют по формуле
Cj характеризует уровень непротиворечивости оценок при составлении матриц парных сравнений.
При выборе изделий (процессов) или при определении предпочтительности взаимозаменяемых или близких по функциональному назначению изделий можно использовать метод простого аддитивного взвешивания. При этом для каждого (/-го) изделия составляются обобщенные оценки:
/=i
где gjt - количественная оценка /-го изделия
(процесса) с точки зрения у-го показателя.
В общем случае для того, чтобы соотношения носили более универсальный характер, исходные оценки gjt нормируют.
Глава 1.13
МЕТРОЛОГИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ИЗМЕРЕНИЙ
Мегрологическое обеспечение измерений включает установление и применение технических средств, правил и норм, необходимых для достижения единства и требуемой точности измерений.
Под единством измерений понимают такое состояние измерений, при котором результаты измерений выражены в узаконенных единицах, а погрешности известны с заданной вероятностью.
Государственная система обеспечения единства измерений - это комплекс регламентированных стандартами взаимоувязанных правил и положений, требований и норм, определяющих организацию и методику проведения работ по оценке и обеспечению точ-
ности измерении, результаты которых используются государственными органами, предприятиями и учреждениями страны.
Аналогичные задачи стоят перед отраслевой и любой другой системой обеспечения единства измерений.
В государственной системе обеспечения единства измерений регламентации подлежат:
-единицы физических величин;
-методы и средства воспроизведения единиц физических величин (в частности, государственные эталоны);
-методы и средства передачи размеров единиц физических величин рабочим средствам измерений, обеспечивающие необходимую точность передачи (в частности, поверочные схемы);
-номенклатура, способы выражения и количественные значения нормируемых метрологических характеристик средств измерений;
-организация, порядок и методика проведения государственных испытаний средств измерений;
-организация, порядок и методика проведения поверки, ревизии и экспертизы, обеспечивающие необходимый уровень надежности средств измерений и правильность их применения;
-требования к методикам вьшолнения измерений; номенклатуру и способы выражения показателей точности измерений и формы представления результатов измерений, обеспечивающие возможность их сравнительной оценки и совместного использования.
1.13.1. ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ И АНАЛИЗ РАЗМЕРНОСТЕЙ
Понятие физическая величина относят к свойству общему в количественном отношении многим физическим объектам, физическим системам, их состояниям и происходящим в них процессам, но в количественном отношении индивидуальному для каждого объекта системы, состояния или процесса.
Количественное содержание в данном объекте свойства, соответствующего понятию "физическая величина", определяется размером физической величины, оценка которого в виде некоторого числа принятых единиц соответствует значению физической величины.
Различают истинное значение физической величины, которое идеальным образом количественно отражало бы соответствующее свойство, и действительное значение, являющееся лишь оценкой истинного значения, но настолько близкое к нему, что для данной цели может быть использовано вместо него.
Совокупность физических величин, связанных между собой зависимостями, относят к системам физических величин, которые состоят
содержание:
[стр.Введение] [стр.1] [стр.2] [стр.3] [стр.4] [стр.5] [стр.6] [стр.7] [стр.8] [стр.9] [стр.10] [стр.11] [стр.12] [стр.13] [стр.14] [стр.15] [стр.16] [стр.17] [стр.18] [стр.19] [стр.20] [стр.21] [стр.22] [стр.23] [стр.24] [стр.25] [стр.26] [стр.27] [стр.28] [стр.29] [стр.30] [стр.31] [стр.32] [стр.33] [стр.34] [стр.35] [стр.36] [стр.37] [стр.38] [стр.39] [стр.40] [стр.41] [стр.42] [стр.43] [стр.44] [стр.45] [стр.46] [стр.47] [стр.48] [стр.49] [стр.50] [стр.51] [стр.52] [стр.53] [стр.54] [стр.55] [стр.56] [стр.57] [стр.58] [стр.59] [стр.60] [стр.61] [стр.62] [стр.63] [стр.64] [стр.65] [стр.66] [стр.67] [стр.68] [стр.69] [стр.70] [стр.71] [стр.72] [стр.73] [стр.74] [стр.75] [стр.76] [стр.77] [стр.78] [стр.79] [стр.80] [стр.81] [стр.82] [стр.83] [стр.84] [стр.85] [стр.86] [стр.87] [стр.88] [стр.89] [стр.90] [стр.91] [стр.92] [стр.93] [стр.94] [стр.95] [стр.96] [стр.97] [стр.98] [стр.99] [стр.100] [стр.101] [стр.102] [стр.103] [стр.104] [стр.105] [стр.106] [стр.107] [стр.108] [стр.109] [стр.110] [стр.111] [стр.112] [стр.113] [стр.114] [стр.115] [стр.116] [стр.117] [стр.118] [стр.119] [стр.120] [стр.121] [стр.122] [стр.123] [стр.124] [стр.125] [стр.126] [стр.127] [стр.128] [стр.129] [стр.130] [стр.131] [стр.132] [стр.133] [стр.134] [стр.135] [стр.136] [стр.137] [стр.138] [стр.139] [стр.140] [стр.141] [стр.142] [стр.143] [стр.144] [стр.145] [стр.146] [стр.147] [стр.148] [стр.149] [стр.150] [стр.151]
