страница - 132
18.2. Расчет винтовых пружин на прочность
Пружины сжатия навивают с просветом между витками. Для образования опорной поверхности, перпендикулярной к продольной оси пружины, крайние витки поджимают и сошлифовывают
(см. рис. 18.1, а и рис. 18.2). Пружины растяжения обычно навивают без просвета между витками. Для соединения с другими деталями на концах пружины образуют зацепы в виде изогнутых витков (см. рис. 18.1, в).
Из рассмотрения равновесия отсеченной части пружины (см. рис. 18.2) можно установить, что в сечении витка действует крутящий момент T—FD0/2 и поперечная сила Q = F (последняя не показана потому, что напряжения сдвига от этой силы незначительны и их при расчете учитывают поправочным коэффициентом). Таким образом, винтовые пружины рассчитывают на кручение.
Условие прочности для пружин из проволоки круглого сечения имеет вид:
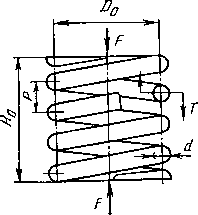
Рис. 18.2. Пружина сжатия с поджатыми и со-шлифованными крайними витками
р
8FD.
nd*
= k
8Fc nd2
(18.1)
где k — поправочный коэффициент, учитывающий влияние кривизны витков и поперечной силы, принимаемый по табл. 18.4; F — осевая нагрузка пружины; D0 — средний диаметр витков пружины; d—диаметр проволоки; с — индекс пружины: c=D0ld; [т] — допускаемое напряжение (см. табл. 18.2).
Зазор между витками во избежание соприкосновения их при сжатии пружины б0,Ы.
На рис. 18.2 показан шаг пружины Р.
Для пружин растяжения с зацепами в виде отогнутых витков значения [т] следует снижать примерно на 25 %.
При проектировочном расчете диаметр проволоки, из которой свита пружина, определяют по формуле
d = 1,61/" kFc/[x].
После определения диаметра по формуле окончательное значение d выбирают по ГОСТу для пружинной проволоки.
Выбирая индекс пружины, следует придерживаться следующей рекомендации: при диаметрах d (мм) до 2,5; 3...5; 6... 12 с соответственно равен 5...12; 4...10; 4...9.
Конические пружины сжатия из проволоки круглого сечения (см. рис. 18.1, г) рассчитывают на прочность по формуле (18.1) по витку с наибольшим диаметром.
Условие прочности для пружин с витками прямоугольного сечения:
Тпгах=*п-- <[Т],(18.2)
где kn — поправочный коэффициент, принимаемый по табл. 18.5; с — индекс пружины: c = D0/a; а — размер сечения витка, параллельного оси пружины; А — площадь поперечного сечения витка.
При расчете пружин кручения с малыми углами подъема (см. рис. 18.1, ж) учитывают возникающие в поперечных сечениях изгибающие моменты. Условие прочности:
amax = £K-<[or],(18-3)
где М — изгибающий момент, примерно равный закручивающему: ММ0\ М0 — момент закручивающей пары; W—момент сопротивления поперечного сечения витков при изгибе; для пружин из проволоки круглого сечения №=jrd3/32; [о] — допускаемое напряжение, принимаемое на 25 % выше, чем [т] для пружины сжатия; kK— поправочный коэффициент при расчете пружин на кручение, зависящий от кривизны витков; его принимают для витков круглого сечения по приближенной зависимости: kK— (4с— 1)/(4с—4).
Расчет на усталость состоит в определении коэффициента запаса прочности sr и сравнении его с требуемым [Sr]. Условие прочности: Sr[SR\.
Запас прочности определяют из формулы
1ттах
где Ттах — максимальное напряжение при кручении; тв — предел прочности материала пружины при сдвиге; ТцОав; R— коэффициент асимметрии цикла: i?=Tmin/Tmax, при расчете пружин предполагают 0<R<\; то — предел выносливости при отнулевом (пульсирующем) цикле.
Требуемый коэффициент запаса прочности [sr} = 1,5...2,2.
18.3. Расчет винтовых пружин на жесткость
Изменение высоты пружины растяжения-сжатия из проволоки круглого сечения определяют по формуле
8FDln8Fc3n
К =-т— =-,(18.5)
рGd4Gdv
где п—число рабочих витков пружины; у пружин сжатия рабочее
число витков на 1,5...2 меньше полного числа витков П\ из-за того,
что крайние витки поджимают и сошлифовывают (см. рис. 18.1, а
и рис. 18.2), они практически в деформации пружины не участвуют;
G — модуль сдвига (для стали G = 8-104 МПа).
Для пружин из прутка прямоугольного сечения
FDlnA
х--cSi—(18-6)
где Л — вспомогательный коэффициент, принимаемый в зависимости от отношения размеров сечения (табл. 18.6); b — меньшая сторона поперечного сечения витков пружины.

(3
Pwc. 18.3. Винтовые цилиндрические пружины сжатия при H0/D0>3:
а — пружина потеряла продольную устойчивость; б — пружины смонтированы на оправке или в гильзе
Во избежание потери продольной устойчивости и выпучивания витков (рис. 18.3, а) общая высота пружины сжатия #о не должна превосходить диаметр D0 более чем в три раза. При значениях H0/D0>3 пружины рекомендуют устанавливать на оправках или в гильзах (рис. 18.3, б).
В пружинах кручения торцевые сечения поворачиваются друг относительно друга. Угол взаимного поворота торцевых сечений пружин из проволоки круглого сечения определяют по формуле
Ф»-:L-:L-.(18.7)
т Ed4v
где MQ — закручивающий момент; Е — модуль продольной упругости (для стали £ = 2,15-105 МПа).
18.4. Подбор тарельчатых пружин
В зависимости от характера нагружения тарельчатые пружины разделены на два класса:
Класс пружины
Нагружение
Выносливость в циклах, не менее
I
II
Циклическое
Статическое и циклическое
2.10е 10*
В связи со сложностью точного расчета тарельчатых пружин их обычно подбирают по таблицам. В ГОСТ 3057—79 помещена методика определения параметров тарельчатых пружин и их количества в комплекте при заданной нагрузке. В приложении к ГОСТу приведены формулы для расчета и примеры выбора тарельчатых пружин I и II классов.
ГОСТ 3057—79 предусматриваются пружины с наружным диаметром 10...400 мм. Изготовляют тарельчатые пружины обычно из стали марки 60С2А по ГОСТ 14959—79.
18.5. Справочный материал
Табл. 18.1. Классификация цилиндрических винтовых пружин
Класс пружины
Вид нагрузки
Характер нагружения
Выносливость в циклах, не менее
Соударение витков
IСжатие и растяжение
IIСжатие и растяжение
IIIСжатие
Циклическое
Циклическое статическое Циклическое
5-10е 1-10» 2 103
Отсутствует Отсутствует Возможно
содержание:
[стр.Введение] [стр.1] [стр.2] [стр.3] [стр.4] [стр.5] [стр.6] [стр.7] [стр.8] [стр.9] [стр.10] [стр.11] [стр.12] [стр.13] [стр.14] [стр.15] [стр.16] [стр.17] [стр.18] [стр.19] [стр.20] [стр.21] [стр.22] [стр.23] [стр.24] [стр.25] [стр.26] [стр.27] [стр.28] [стр.29] [стр.30] [стр.31] [стр.32] [стр.33] [стр.34] [стр.35] [стр.36] [стр.37] [стр.38] [стр.39] [стр.40] [стр.41] [стр.42] [стр.43] [стр.44] [стр.45] [стр.46] [стр.47] [стр.48] [стр.49] [стр.50] [стр.51] [стр.52] [стр.53] [стр.54] [стр.55] [стр.56] [стр.57] [стр.58] [стр.59] [стр.60] [стр.61] [стр.62] [стр.63] [стр.64] [стр.65] [стр.66] [стр.67] [стр.68] [стр.69] [стр.70] [стр.71] [стр.72] [стр.73] [стр.74] [стр.75] [стр.76] [стр.77] [стр.78] [стр.79] [стр.80] [стр.81] [стр.82] [стр.83] [стр.84] [стр.85] [стр.86] [стр.87] [стр.88] [стр.89] [стр.90] [стр.91] [стр.92] [стр.93] [стр.94] [стр.95] [стр.96] [стр.97] [стр.98] [стр.99] [стр.100] [стр.101] [стр.102] [стр.103] [стр.104] [стр.105] [стр.106] [стр.107] [стр.108] [стр.109] [стр.110] [стр.111] [стр.112] [стр.113] [стр.114] [стр.115] [стр.116] [стр.117] [стр.118] [стр.119] [стр.120] [стр.121] [стр.122] [стр.123] [стр.124] [стр.125] [стр.126] [стр.127] [стр.128] [стр.129] [стр.130] [стр.131] [стр.132] [стр.133] [стр.134]
