страница - 47
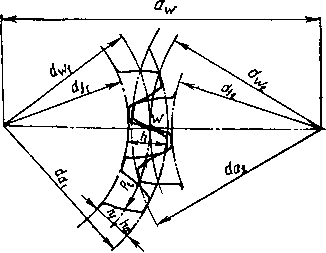
Рис. 9.3. Эвольвентное некорригирован-ное зацепление
ности зубчатого колеса. Шаг складывается из толщины зуба и ширины впадины между зубьями.
Головка зуба (высоту делительной головки зуба обозначают ha) — часть зуба между делительной окружностью зубчатого колеса и окружностью вершин зубьев.
Н ожка зуба (высоту делительной ножки зуба обозначают hf) — часть зуба, расположенная между делительной окружностью и окружностью впадин.
Высота зуба h=ha+ + hf.
Окружность вершин зубьев (ее диаметр da) — окружность, ограничивающая головки зубьев.
Окружность впадин (ее диаметр df) — окружность, проходящая через основания впадин зубьев.
Дугазацепления L — путь по начальной окружности, проходимый точкой профиля зуба за время зацепления пары сопряженных зубьев.
Коэффициент пере-крытияе — отношение дуги зацепления к шагу: z — Ljpt.
Для непрерывной работы необходимо, чтобы до выхода из зацепления работающей пары зубьев в него вошла еще одна пара. Это произойдет, если дуга зацепления будет больше шага. Чем больше коэффициент перекрытия, тем больше пар зубьев могут одновременно находиться в зацеплении и тем плавнее работает передача. Коэффициент перекрытия показывает, сколько пар зубьев в среднем находится в зацеплении; так, при 8= 1,4 в течение 40 % продолжительности зацепления находятся две пары зубьев, а 60% — одна.
Для непрерывной и плавной работы передачи должно быть е>1 (лучше е>1,2).
Межосевое расстояние aw — сумма радиусов начальных окружностей шестерни и колеса:
aw={dwl+dw2)/2.(9.1)
Числа зубьев шестерни и колеса обозначают гх и z2. Модуль зацепления — отношение шага к числу я, т. е. m = pt/n.
Модули 0,05... 100 мм стандартизованы (см. табл. 9.1). Диаметры окружностей:
dw = mz\
da=dw + 2ha = dw -+ 2m*;(9.2)
df — dw — 2hj — dw — 2,5m*. J
* У колес с укороченным зубом ha — 0,8mt a h(=m.
Межосевое расстояние [см. формулу (9.1)]
aw=[m(zi+22)]/2 = 0,5 mze,
где ze — суммарное число зубьев: zc = Z\+z2.
Передаточное отношение понижающей передачи равно ее передаточному числу:
где coi, ©2 — угловые скорости, рад/с; яь п2— частота вращения соответственно шестерни и колеса, мин-1.
Передаточное число понижающей передачи и=z2\zx.
а56

Рис. 9.4. Зависимость формы зубьев от их числа
Передаточные числа одноступенчатой зубчатой передачи в закрытом корпусе могут достигать для цилиндрической пары 10, многоступенчатой — нескольких сот.
При выборе числа зубьев следует иметь в виду, что с уменьшением их числа уменьшается толщина зуба у основания и у вершины (рис. 9.4, а, б), что приводит к понижению его прочности на изгиб. Поэтому не рекомендуют выбирать число зубьев меньше, чем zm\n. При числе зубьев z<zmm происходит подрезание ножки зуба (рис. 9.4, в), что приводит к резкому снижению прочности. При нарезании зубьев инструментом реечного типа zmin=17. В редукторах рекомендуют принимать для первой ступени zx=22...36, для второй и третьей ступеней Zi = 18...26.
В колесах с косым зубом (рис. 9.5, а) различают окружной шаг Pt, который измеряется параллельно торцу колеса (рис. 9.5, б), и нормальный шаг рп, измеряемый в нормальном к направлению зуба сечении:
Pn=p*cos р,
где р — угол наклона зуба. Во избежание больших осевых усилий принимают р = 8...15° (редко до 20°).
Аналогично связаны между собой нормальный тп и окружной rrit модули:
mn = mtcos р.
По стандарту выравнивают обычно нормальный модуль (см. табл. 9.1).
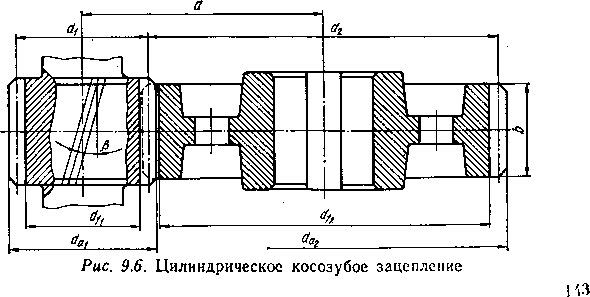
Диаметры окружностей и межосевое расстояние косозубых передач:
dw = rritz; da—dw-\- 2m„; df = dw — 2,5m,,;,
(9.3)
Ow =
mt (2j -4- 22)
mn*c
(9.4)
22 cos p*
где zc=zl+z2.
Профиль косого зуба в нормальном сечении совпадает с профилем зуба на прямозубом колесе. Расчет косозубых колес ведут, используя параметры так называемого эквивалентного прямозубого колеса (рис. 9.5, в) с радиусом начальной окружности, равным ра-
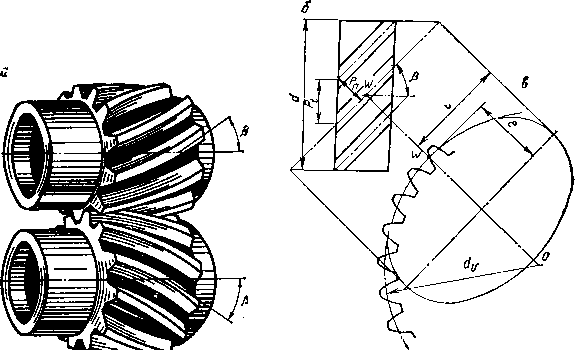
Рис. 9.5. Косозубые колеса:
а — колеса в зацеплении; б — схематическое изображение косозубого колеса: в — эквивалентное колесо
содержание:
[стр.Введение] [стр.1] [стр.2] [стр.3] [стр.4] [стр.5] [стр.6] [стр.7] [стр.8] [стр.9] [стр.10] [стр.11] [стр.12] [стр.13] [стр.14] [стр.15] [стр.16] [стр.17] [стр.18] [стр.19] [стр.20] [стр.21] [стр.22] [стр.23] [стр.24] [стр.25] [стр.26] [стр.27] [стр.28] [стр.29] [стр.30] [стр.31] [стр.32] [стр.33] [стр.34] [стр.35] [стр.36] [стр.37] [стр.38] [стр.39] [стр.40] [стр.41] [стр.42] [стр.43] [стр.44] [стр.45] [стр.46] [стр.47] [стр.48] [стр.49] [стр.50] [стр.51] [стр.52] [стр.53] [стр.54] [стр.55] [стр.56] [стр.57] [стр.58] [стр.59] [стр.60] [стр.61] [стр.62] [стр.63] [стр.64] [стр.65] [стр.66] [стр.67] [стр.68] [стр.69] [стр.70] [стр.71] [стр.72] [стр.73] [стр.74] [стр.75] [стр.76] [стр.77] [стр.78] [стр.79] [стр.80] [стр.81] [стр.82] [стр.83] [стр.84] [стр.85] [стр.86] [стр.87] [стр.88] [стр.89] [стр.90] [стр.91] [стр.92] [стр.93] [стр.94] [стр.95] [стр.96] [стр.97] [стр.98] [стр.99] [стр.100] [стр.101] [стр.102] [стр.103] [стр.104] [стр.105] [стр.106] [стр.107] [стр.108] [стр.109] [стр.110] [стр.111] [стр.112] [стр.113] [стр.114] [стр.115] [стр.116] [стр.117] [стр.118] [стр.119] [стр.120] [стр.121] [стр.122] [стр.123] [стр.124] [стр.125] [стр.126] [стр.127] [стр.128] [стр.129] [стр.130] [стр.131] [стр.132] [стр.133] [стр.134]
