страница - 61
Коэффициенты:
ZM = 275 (Н/мм2)1/2; Z[{ = 1,77 cos p* = 1,77 • 0,97826 = 1,73; ea = [l ,88 - 3,2 (j- + -I)] cos 0 = [, ,88 - 3.2 (JL + -L)] 0,97826 = 1,7;
Коэффициент Кн Кна.КHv где на~ "»08 по табл. 9.12; /Ся = = 1,08 по табл. 9.11; KHv— 1 (особой точности не требуется): /(я = 1,08 X X 1,08 • 1 = 1,17.
Контактное напряжение:
if 2 • 2 • 106 • 1,17 . 6 он = 275 • 1,73 • 0,79 j/ -383.3У > 115-= 477 МПа>
т# е. меньше, чем [ан] = 503 МПа. Прочность обеспечена.
15. Выполняем проверочный расчет на усталость при изгибе по формуле (9.44). По табл. 9.10 определяем значения коэффициентов YF, учитывающих форму вуба, в зависимости от эквивалентного числа зубьев при х = 0:
zv{ = /cos3 р = 25/0,978263 « 27;
*v2 = z2/cos3 р = 125/0,978263 ~ 135.
По эквивалентному числу зубьев 2=27 YFl = 3,86 и по эквивалентному числу
вубьев zv2 = 135 YF2 = 3,6.
Расчет следует выполнить для того зубчатого колеса, у которого меньше отношение [oF]/YF*
В нашем случае:
[oF]{/YFl = 465/3,86 = 120; [oF]2/YF2 = 425/3,6 = 118.
Расчет проводим по колесу.
Коэффициент Ys — 1 [см. пояснения к формуле (9.44)]. Коэффициент Y = 1 — (5/140 для косозубых колес:
1Г5820"
,40 °°-914-
Коэффициент KF — FaFFv где Fa ~ коэффициент, учитывающий распределение нагрузки между зубьями:
4 + (ea-l)(s-5) 4 + (1,7-1) (8-5) KFa=4=4.1,7=0,9.
Коэффициент KF$ учитывает распределение нагрузки по ширине венца и определяется по табл. 9.11 в зависимости от tybd. В нашем случае KF = = аКир> = 1,1 • 1,08= 1,19.
Коэффициент KFv учитывает динамическую нагрузку, возникающую в зацеплении, и определяется по табл. 9ЛЗ: /(/?<, = 1,3. Тогда KF = 0,9 • 1,19 х
X 1,3= 1,4.
Напряжение при изгибе
а = 2 . 3,6 . 1 . 0,914 • 2 • 10е • 1,4/(125 . 115 • З2) = 142 МПа,
V* е. меньше, чем [oF]2 = 425 МПа. Условие прочности выполнено.
В результате аналогичного расчета закрытой передачи цилиндрическими зубчатыми колесами по тем же исходным данным получаются следующие результаты: межосевое расстояние — 300 мм, модуль— 4 мм, ширина колеса — 150 мм. Таким образом, косозубая передача оказывается выгоднее прямозубой (по габаритам и массе).
Пример 9.2. Закрытая реверсивная коническая прямозубая передача предназначена для трехсменной работы в течение четырех лет. Шестерня расположена на консоли (рис. 9.22).
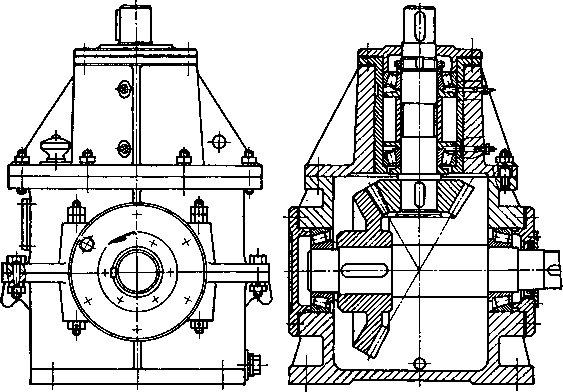
Рис. 9.22. Конический редуктор с вертикальным ведущим валом
Рассчитать передачу по следующим данным: момент на зубчатом колесе Т2= 40 • 103 Н • мм, коэффициент г = 0,3, частота вращения шестерни пх =
= 740 мин""1, колеса п2 = 375 мин"""1.
Параметры передачи должны быть согласованы с ГОСТом.
Сравнить расчетные значения de2, характеризующие размеры передачи прямозубой и с круговым зубом.
Решение. 1. Так как материалы для шестерни и для колеса не заданы, их следует выбрать по табл. 9.6.
Для шестерни принимаем сталь 45 улучшенную, твердостью примерно 230 НВ, а для колеса — сталь 45 нормализованную, твердостью примерно 210 НВ (принимаем средние значения из приведенных в таблице).
2. Суммарное число циклов перемен напряжений для зубчатого колеса при продолжительности работы 3-7 = 21 ч в течение 300 рабочих дней в году
N2 = 60n2LA.
Здесь Lh = 21 • 300 • 4 = 25 200 ч — срок службы за 4 года.
#2 = 60 . 375 - 25 200 = 565 - 106.
База испытаний при твердости стали 210 НВ (см. рис. 9.12) составляет NHG ~ И • Ю6. Для колеса N% > NHG. Для шестерни, которая вращается быстрее, тем более NIt>NHQ. При этом условии коэффициент долговечности KHL— 1 [см. пояснения к формуле (9.8)].
3.Пределы контактной выносливости по табл. 9.8 для шестерни и для колеса:
°н ltm bt = 2 НВ + 70 = 2 - 230 + 70 = 530 МПа»
°Н lim Ь* = 2 НВ + 70 = 2 • 210 + 70 = 490 МПа-
4.Допускаемые контактные напряжения для шестерни и для колеса определяются по формуле (9.10), где SH = 1,1 (см. пример 9.1).
Для шестерни [ая], =0,9 • 530 • 1/1,1 = 432 МПа.
Для колеса [он]2 = 0,9 • 490 • 1/1 ,1 = 400 МПа.
Для прямозубых передач принимают окончательно меньшее значение, т. е. ]°н]пР = 40° МПа.
Для передач с криволинейными зубьями принимают условное допускаемое напряжение [см. формулу (9.11)]
[ая]кР = °>5 ([°и]\ + [анЪ) = °>5 <432 + 40°) = 416 МПа.
При этом должно быть выполнено требование [<*//]кр < 1,25 [ff//]min (416 < 1,25 • 400).
Поэтому окончательно для колес с криволинейными зубьями (в нашем случае с круговыми зубьями) принимаем допускаемое контактное напряжение
[*я]кр = 416 МПа.
5.Допускаемые напряжения при изгибе [см. формулу (9.14)}
[°>] = (°>Jim 6KfJsf) Kfc-По табл. 9.8 для шестерни и колеса:
°> hmbl = НВ + 260 = 230 + 260 = 490 МПа: °> ИтЬг = НВ -f 260 = 210 + 260 = 470 МПа.
Коэффициент безопасности 5F= 1,8 [см. пояснения к формуле (9.14)]; принимаем значение коэффициента долговечности KFL=\,b и значение коэффициента, учитывающего влияние реверсивной нагрузки, KFc — 0,75.
Тогда допускаемые напряжения при изгибе для шестерни и колеса:
490 • 1,5
[°>h = —7~r—°>75 = 303 мпа;
470 • 1,5
\(jF]2 =-——0,75 = 294 МПа.
1,8
6.Передаточное число и=ni!n2=740/375= 1,975.
7.Внешний делительный диаметр большего конического колеса определяется по формуле (9.40).
«n i3 Г 40 • 103 • 1 • 1,975 = "/ 4002 (1 -0,5.0,3)2 0,3 =И8 ММ Для конических передач с круговыми зубьями /Свб; в этом случае
* / 40 - 103 • 1 • 1,975
dpcy = 86 I/ лщг%9 у%-—— „ 9 „— = 126 мм.
е2 у 4162 (1 —0,5 . 0,3)2 0,3
Сравнивая полученные результаты, можно сделать вывод, что коническая передача с круговыми зубьями имеет меньший расчетный параметр de2 по сравнению с передачей, имеющей прямые зубья. Это уменьшение составляет [(148 — -126)/148]100~15 %.
Дальнейший расчет проведем для прямозубой передачи.
8.Примем число зубьев шестерни 2, = 32.
9.Число зубьев зубчатого колеса г2=г1«=32- 1,975=63,3. Принимаем г2в64.
содержание:
[стр.Введение] [стр.1] [стр.2] [стр.3] [стр.4] [стр.5] [стр.6] [стр.7] [стр.8] [стр.9] [стр.10] [стр.11] [стр.12] [стр.13] [стр.14] [стр.15] [стр.16] [стр.17] [стр.18] [стр.19] [стр.20] [стр.21] [стр.22] [стр.23] [стр.24] [стр.25] [стр.26] [стр.27] [стр.28] [стр.29] [стр.30] [стр.31] [стр.32] [стр.33] [стр.34] [стр.35] [стр.36] [стр.37] [стр.38] [стр.39] [стр.40] [стр.41] [стр.42] [стр.43] [стр.44] [стр.45] [стр.46] [стр.47] [стр.48] [стр.49] [стр.50] [стр.51] [стр.52] [стр.53] [стр.54] [стр.55] [стр.56] [стр.57] [стр.58] [стр.59] [стр.60] [стр.61] [стр.62] [стр.63] [стр.64] [стр.65] [стр.66] [стр.67] [стр.68] [стр.69] [стр.70] [стр.71] [стр.72] [стр.73] [стр.74] [стр.75] [стр.76] [стр.77] [стр.78] [стр.79] [стр.80] [стр.81] [стр.82] [стр.83] [стр.84] [стр.85] [стр.86] [стр.87] [стр.88] [стр.89] [стр.90] [стр.91] [стр.92] [стр.93] [стр.94] [стр.95] [стр.96] [стр.97] [стр.98] [стр.99] [стр.100] [стр.101] [стр.102] [стр.103] [стр.104] [стр.105] [стр.106] [стр.107] [стр.108] [стр.109] [стр.110] [стр.111] [стр.112] [стр.113] [стр.114] [стр.115] [стр.116] [стр.117] [стр.118] [стр.119] [стр.120] [стр.121] [стр.122] [стр.123] [стр.124] [стр.125] [стр.126] [стр.127] [стр.128] [стр.129] [стр.130] [стр.131] [стр.132] [стр.133] [стр.134]
