страница - 64
В табл. 10.1 приведены рациональные предельные значения передаточных отношений, формулы для определения передаточных отношений, частот вращения их сателлитов и коэффициентов полезного действия.
10.3. Условия собираемости соосных и многопоточных передач
Планетарные передачи обычно соосные и многопоточные (передача на схеме 3 — однопоточная). Поэтому при выборе чисел зубьев колес для обеспечения их собираемости необходимо выполнять следующие условия.
1.Условие соосности. Для передач, изображенных на рис. 10.1...10.3 (схемы 1, 2 табл. 10.1 и им аналогичные),
Если колеса нарезаны без смещения инструмента,
Z1 Л~ Z2 = Z$ — Z2
или
zz=zx+2z2\ z2 = (zs-Zi)/2.(Ю.5)
Для передачи, показанной на схеме 3 табл. 10.1,
aw\2 = aW23.(10.6)
Если модули колес обеих ступеней (1; 2 и 2; 3) равны и зубья нарезены без смещения инструмента,
Z\ — z2 = z3 — z2>.(Ю.7)
В сложных передачах в зависимости от схемы для каждой ступени справедливо одно из приведенных выше уравнений.
В многопоточных передачах, кроме условия соосности, необходимо выполнять еще два условия собираемости.
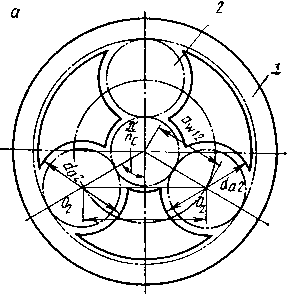
2.Условие соседства. Для того чтобы соседние сателлиты не задевали зубьями друг друга, необходимо выполнять условие (рис. 10.6, а)
0202> > da2,
где 0202 — межосевое расстояние между соседними сателлитами; dU2 — диаметр окружности вершин сателлитов,
или
2awi2sin(jT/nc)>da2(10.8)
где aw\2 — межосевое расстояние между солнечным колесом / и сателлитом 2\ пс — число сателлитов.
Если колеса нарезаны без смещения инструмента (хх=х2= = *з=0),
{zx+z2) sin (я/пс) > z2 + 2,5.(10.9)
Минимальное значение разности чисел зубьев определяется условиями вентиляции и смазывания передачи, но оно не должно быть меньше 2 мм. Для передач, где т>2, минимальное значение этой разности обычно принимают равным модулю передачи.
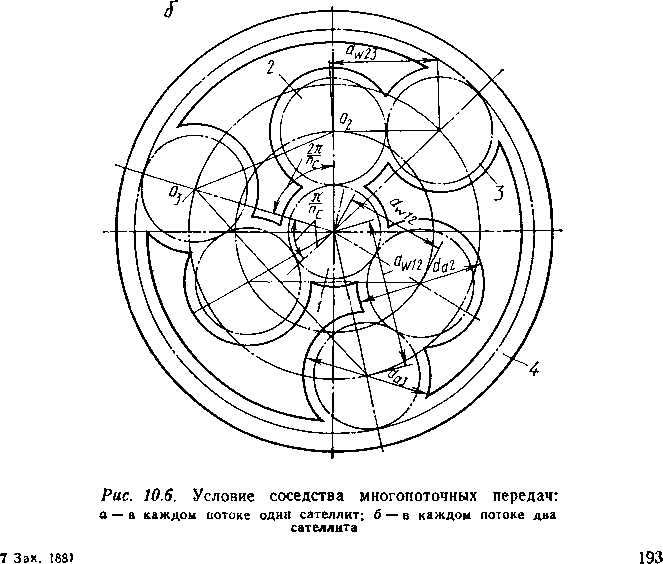
Для передачи, приведенной на схеме 4 табл. 10.1, условие соседства записывается в виде пяти неравенств (см. рис. 10.6, б: 1— солнечное колесо; 2, 3 — сателлиты; 4 — корончатое колесо):
da2 < 2awi2 sin (я/лс); da3 < 2аюз4 sin (я/яс);
da2 + 4a < 20203; }(10.10)
dai — daa <C 2oo,i2; do 4 — da3 <C 2ашз4«
3. Условие вхождения зубьев в зацепление при равенстве центральных углов расположения сателлитов. Для передач, изображенных на рис, 10.1...10.3 и схемах 1 и 2 табл. 10.1 и им аналогичных с одновенцовыми сателлитами,
(zi+zs)/nc
или 2{гх+г2)/пс = целое число.(10.11)
Для передачи, приведенной на схем« 4 табл. 10.1,
(zi+zA)/nc = целое число.(10.12)
В передачах с двухвенцовыми сателлитами для упрощения подбора чисел зубьев и сборки передачи числа зубьев всех центральных колес выбирают кратными числу сателлитов.
10.4. Порядок подбора чисел зубьев при заданном передаточном отношении и числе сателлитов
Для передач, показанных на рис. 10.1...10.3 и схемах 1, 2 к табл. 10.1, и соответствующих им ступеней (схемы 6, 7 и 8 табл. 10.1):
1)задаемся числом зубьев солнечного колеса 1. Из условия отсутствия практически заметного ослабления прочности на изгиб зубьев из-за их подрезания Zil3;
2)число зубьев сателлита zi — Z\ (iш—2)/2 (округляется до ближайшего целого числа);
3)проверяем условие вхождения зубьев в зацепление при заданном числе сателлитов: 2(21+г2)/пс = целое число.
Если это условие не выполняется, следует увеличить или уменьшить число зубьев одного или обоих колес (лучше имеющего большее число зубьев);
4)находим из условия соосности число зубьев корончатого колеса 3 (см. рис. 10.6, a): Zz = zx+2z2.
5)определяем фактическое передаточное отношение при выбранных числах зубьев и отклонение его от заданного. В ГОСТ 25022—81 «Редукторы планетарные. Основные параметры» допускается отклонение фактического передаточного отношения от номинального не более чем на 4 % для одноступенчатых редукторов, 5 % — двухступенчатых и 6,3 % — для трехступенчатых.
При подборе чисел зубьев мотор-редуктора удобнее другой порядок:
1)определяем число зубьев корончатого колеса 3 z3=d5/m (диаметр d3 выбирается исходя из диаметра фланца присоединяемого электродвигателя, а модуль—по технологическим соображениям);
2)число зубьев солнечного колеса / zx = z3/(i{)}— l);
3)число зубьев сателлита z2 = (z3—Zi)/2;
4)проверяем условие вхождения зубьев в зацепление при рав-
содержание:
[стр.Введение] [стр.1] [стр.2] [стр.3] [стр.4] [стр.5] [стр.6] [стр.7] [стр.8] [стр.9] [стр.10] [стр.11] [стр.12] [стр.13] [стр.14] [стр.15] [стр.16] [стр.17] [стр.18] [стр.19] [стр.20] [стр.21] [стр.22] [стр.23] [стр.24] [стр.25] [стр.26] [стр.27] [стр.28] [стр.29] [стр.30] [стр.31] [стр.32] [стр.33] [стр.34] [стр.35] [стр.36] [стр.37] [стр.38] [стр.39] [стр.40] [стр.41] [стр.42] [стр.43] [стр.44] [стр.45] [стр.46] [стр.47] [стр.48] [стр.49] [стр.50] [стр.51] [стр.52] [стр.53] [стр.54] [стр.55] [стр.56] [стр.57] [стр.58] [стр.59] [стр.60] [стр.61] [стр.62] [стр.63] [стр.64] [стр.65] [стр.66] [стр.67] [стр.68] [стр.69] [стр.70] [стр.71] [стр.72] [стр.73] [стр.74] [стр.75] [стр.76] [стр.77] [стр.78] [стр.79] [стр.80] [стр.81] [стр.82] [стр.83] [стр.84] [стр.85] [стр.86] [стр.87] [стр.88] [стр.89] [стр.90] [стр.91] [стр.92] [стр.93] [стр.94] [стр.95] [стр.96] [стр.97] [стр.98] [стр.99] [стр.100] [стр.101] [стр.102] [стр.103] [стр.104] [стр.105] [стр.106] [стр.107] [стр.108] [стр.109] [стр.110] [стр.111] [стр.112] [стр.113] [стр.114] [стр.115] [стр.116] [стр.117] [стр.118] [стр.119] [стр.120] [стр.121] [стр.122] [стр.123] [стр.124] [стр.125] [стр.126] [стр.127] [стр.128] [стр.129] [стр.130] [стр.131] [стр.132] [стр.133] [стр.134]
