страница - 65
ных центральных углах расположения сателлитов: (2l + 23)/ttc = =целое число;
5)корректируем число зубьев (если проверка не сошлась);
6)определяем фактическое значение передаточного отношения и его погрешность.
Для предварительного подбора числа зубьев колес рекомендуется использовать табл. 10.2.
Приведенный порядок подбора зубьев относится к передачам, зубчатые колеса которых нарезаны без смещения инструмента.
Применение в передачах солнечных колес и сателлитов, нарезанных с положительным смещением, позволяет увеличить нагрузочную способность передачи и облегчить подбор чисел зубьев (разность z3—Z\ может быть нечетной).
При подборе зубьев передач, показанных на схеме 3 табл. 10.1, подбор чисел зубьев ограничивается только условиями соосности и выполнением заданного передаточного отношения колес, так как
zr4 с-1
е*2
HI
600 500 400
300 250 200
150
100 60 L 60 У 50 40
30 20
10
Шло зу£ье£13 но/теса3 е2
—4. | |||||||||||
е*3
е-4
e-S е6
3
/ | |||||||||||
-А | |||||||||||
I |
е-з
е*4
е-5 e-s
е-д
C(j)
600 500 400 350 300 250 200 150
100 80 60 50 40 JO
20 10
е=2
е*3 е*4
30 40 50 60 70 30 90 Шло зуЛеб Zj колеса!
JO 40 50 60 70 80 90 Шло зу<5ьев Z3 колеса3
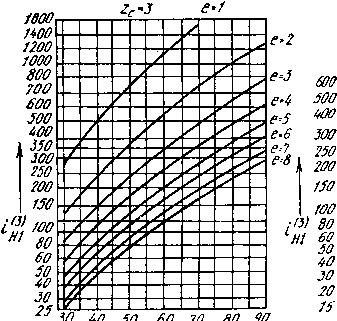
Рис. 10.7. Графики для подбора чисел зубьев планетарных передач по
схеме 3 табл. 10Д
7*
195
эти передачи однопоточные. При равных модулях зацепления колес 1\2 и 2;3 имеем
Z\ — z2 = zs — г2>; zz — Z\ = z2> — z2;
Z2 23
i<3> — 1
;(3) lHl
(10.13) (10.14)
По этим уравнениям, задаваясь значениями разностей
Zc = Z\ — 2г = 2з — Z2 И e — Zz — Z\ = z2> — z2y
определяем z3 по формуле
z3 =
(*c + e) + / (*c + <f + *V (»gl ~ 0
(10.15)
или по рис. 10.7.
Остальные передачи табл. 10.1 представляют собой комбинации рассмотренных схем.
При малой разности чисел зубьев колеса и шестерни внутреннего зацепления zc = {z\—22)min, нарезанных стандартным инструментом, может иметь место пересечение головок зубьев шестерни и колеса, не позволяющее собрать передачу. На рис. 10.8 приведен гра-
8 6
4
ч
40 60 60 100 120 /40 160 180 200 220 //
Рис. 10.8. График для определения минимальной разности чисел зубьев колес внутреннего зацепления
фик для определения минимального значения zc, при котором отсутствует пересечение головок зубьев, в зависимости от числа зубьев колеса с внутренними зубьями.
Если нужно сделать передачу с zc меньшим, чем указано на рис. 10.8, необходимо применять смещение инструмента при нарезании зубьев.
При значении гс 3 можно делать внутреннее зацепление без смещения инструмента, применяя инструмент с углом исходного
профиля а0 = 30° и коэффициентом высоты головки ha = 0,8.
10.5. Определение КПД планетарных передач
КПД планетарных передач зависит от потерь мощности, возникающих при относительном движении колес, т. е. движении при остановленном водиле, когда ведущее колесо k вращается со ско-
ростью со> = co["> — co}J?>, а колесо п, которое было неподвижно в планетарном механизме, вращается со скоростью cow> =—ю:
т№-р№/рР = И"-/>!£)//>Г>. (юле)
При ведущем водиле Я, ведомом колесе k и неподвижном п
ЧЙ - рр/р№ = Pin)/(Pin> + />Ж),(Ю.17)
где Р(н и р£л) — мощность соответственно на водиле и колесе при остановленном колесе п; Р(п"1 — мощность, затрачиваемая на преодоление сопротивлений движению в передаче при остановленном водиле Я.
Потеря мощности в передаче определяется как разность мощностей на ведущем и ведомом звеньях передачи.
Когда со£я> = ю<л> — co<J> > 0,
Р<"> =/><"> /><"> =PiH)=ЯГ*12). (Ю.18)
Когда со" == со<") — со<?> < 0,
ts? = tap =1 - ns? =1 - па? =1 - .... (Ю.20)
где tMW) — коэффициент потерь мощности в планетарной передаче
fx *
при остановленном водиле; г]—КПД пары зубчатых колес с неподвижными осями (с учетом потерь в подшипниках, вентиляционных и на перемешивание масла); р — число зацеплений в передаче.
По экспериментальным данным т]~0,98 (жидкий смазочный материал, опоры на подшипниках качения).
В табл. 10.1 даны формулы для определения КПД приведенных в ней передач и его ориентировочные значения для указанных рациональных пределов передаточного отношения.
10.6. Определение сил, действующих в зацеплениях и в опорах осей и валов прямозубых передач
При определении сил, действующих в зацеплениях и в опорах, как правило, определяют только окружные силы, так как в передачах, где сателлиты входят в зацепление с двумя центральными колесами с наружными и внутренними зубьями, радиальные составляющие, действующие на сателлиты, взаимно уравновешиваются, а окружные суммируются. В многопоточных передачах (если не учитывать ошибки изготовления) силы в зацеплениях, действующие на центральные звенья, также уравновешиваются. Силы трения, действующие в зацеплениях, при силовом расчете не учитывают.
При проведении силового расчета удобно пользоваться методом, показанным на рис. 10.9...10.11, где последовательно рассматрива-
содержание:
[стр.Введение] [стр.1] [стр.2] [стр.3] [стр.4] [стр.5] [стр.6] [стр.7] [стр.8] [стр.9] [стр.10] [стр.11] [стр.12] [стр.13] [стр.14] [стр.15] [стр.16] [стр.17] [стр.18] [стр.19] [стр.20] [стр.21] [стр.22] [стр.23] [стр.24] [стр.25] [стр.26] [стр.27] [стр.28] [стр.29] [стр.30] [стр.31] [стр.32] [стр.33] [стр.34] [стр.35] [стр.36] [стр.37] [стр.38] [стр.39] [стр.40] [стр.41] [стр.42] [стр.43] [стр.44] [стр.45] [стр.46] [стр.47] [стр.48] [стр.49] [стр.50] [стр.51] [стр.52] [стр.53] [стр.54] [стр.55] [стр.56] [стр.57] [стр.58] [стр.59] [стр.60] [стр.61] [стр.62] [стр.63] [стр.64] [стр.65] [стр.66] [стр.67] [стр.68] [стр.69] [стр.70] [стр.71] [стр.72] [стр.73] [стр.74] [стр.75] [стр.76] [стр.77] [стр.78] [стр.79] [стр.80] [стр.81] [стр.82] [стр.83] [стр.84] [стр.85] [стр.86] [стр.87] [стр.88] [стр.89] [стр.90] [стр.91] [стр.92] [стр.93] [стр.94] [стр.95] [стр.96] [стр.97] [стр.98] [стр.99] [стр.100] [стр.101] [стр.102] [стр.103] [стр.104] [стр.105] [стр.106] [стр.107] [стр.108] [стр.109] [стр.110] [стр.111] [стр.112] [стр.113] [стр.114] [стр.115] [стр.116] [стр.117] [стр.118] [стр.119] [стр.120] [стр.121] [стр.122] [стр.123] [стр.124] [стр.125] [стр.126] [стр.127] [стр.128] [стр.129] [стр.130] [стр.131] [стр.132] [стр.133] [стр.134]
