страница - 74
Условие соосности при равных модулях и вхождения зубьев в зацепление во всех зонах
21 — 22 = 23 — 22 = knw,(И.7)
откуда
Zz — Z\=zr—Z2 = e.(11.8)
Решая совместно уравнения (11.5), (11.7)и (11.8) относительно е, получаем
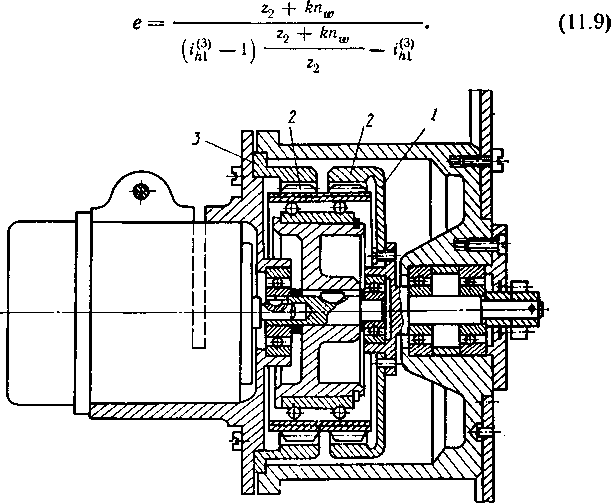
Рис. 11.6. Мотор-редуктор, выполненный по схеме 3 табл. 11.1
Подбор чисел зубьев ведут в следующем порядке:
1)по формуле (Н.9) определяют значение е (значение ij задано, 22 выбирают в пределах 150...600, при двухволновом генераторе k — 1 и nw = 2);
2)определяют числа зубьев остальных колес:
z\ = z2 + knw; z2> = J?2 + e\ z3 = zr + knw,
3)проверяют полученное передаточное отношение и его отклонение от заданного.
Передача (схема 3 табл. 11.1) имеет значительно меньшие осевые габариты по сравнению с простыми волновыми, но и меньшие КПД и нагрузочную способность. Рациональная область применения — приводы кратковременного включения систем управления с передаточным отношением 300...6000.
Передачу, показанную на схеме 3 табл. 11.1, можно преобразовать в простую волновую (схема 2), сделав равными числа зубьев гибкого венца 2 и неподвижного жесткого корончатого колеса 3 (г2> = г3).
В этом случае вместо зацепления получится зубчатое соединение. Такая передача будет иметь меньшие осевые габариты, чем передача, приведенная на схеме 2 табл. 11.1, но на 20...25 % меньший КПД и в 2 раза меньшую нагрузочную способность. На рис. 11.7 изображен общий вид такого редуктора. Левое зацепление является волновым зубчатым соединением.
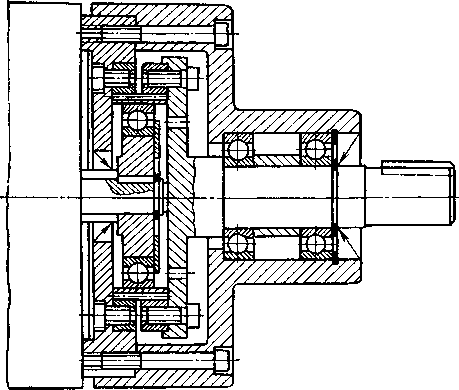
Рис. 11.7. Мотор-редуктор, выполненный по схеме 2 табл. 11.1, с коротким гибким колесом
11.3. Проектный расчет волновой зубчатой передачи
Волновые зубчатые передачи выходят из строя из-за изнашивания поверхностных слоев зубьев, усталостного разрушения гибкого колеса. В передачах с кулачковым генератором с гибким подшипником выход из строя может быть вследствие усталостного разрушения колец сепаратора или усталостного выкрашивания поверхностных слоев беговых дорожек колец и тел качения.
В передачах с роликовыми и дисковыми генераторами следует проверять долговечность подшипников качения роликов или дисков.
Ориентировочно диаметр стального гибкого колеса простой волновой передачи, при котором обеспечиваются контактная прочность рабочих поверхностей зубьев и прочность цилиндрической оболочки,
d2> 1.663/~77~,(11.10)
где d2— предварительное значение делительного диаметра гибкого колеса, мм; Т2 — вращающий момент на ведомом валу, Н • мм.
Толщина гибкого колеса под зубьями из условия его изгибной прочности (ориентировочно)
W = 0,01*4(И.И)
Предварительно внутренний диаметр гибкого колеса определяют по формуле
D= т(22> 3,4),(11.12)
где т — предварительное значение модуля.
Данная формула выведена с учетом принятых коэффициентов
смещения исходного контура, поэтому D > d2. При кулачковом генераторе окончательный диаметр D уточняется после выбора гибкого подшипника.
Диаметр гибкого подшипника из условия обеспечения заданной долговечности
D>2,26(72 • 10-3)°.357[Lft(„ft „2)]o,ii9,(11ЛЗ)
где Г2—вращающий момент на гибком колесе, Н-мм; Lh — заданная долговечность, ч.
При окончательном выборе внутреннего диаметра гибкого колеса должна обеспечиваться зависимость DDf.
По наружному диаметру подшипника (см. табл. 11.2) определяют значение модуля, решая уравнение (11.12) относительно т.
Толщина стенки гибкого колеса под зубьями
h = т [0,512 -}- 3 — (hi + с*) ] — 0,5D.(11.14)
Проверочный расчет на прочность гибкого колеса выполняют после определения основных параметров передачи [7]. Проверяется коэффициент запаса по нормальным напряжениям:
So=-—->[s0),(11.15)
где Ka—коэффициент, учитывающий отличие теоретических коэффициентов концентрации от эффективных: Ко = (1 + АтЛт-i)-1. Значения Аа см. в табл. 11.3; ра — коэффициент, учитывающий состояние поверхности.
Для случая деформирования гибкого колеса по эллипсу на ве-* личину w
w=Kwtn cos (2ф); оа = 0,35аи+4,93£/im/p2; от = 0,35аи+0,214£Лт/р2,
где Е — модуль упругости: для стали £=2,15-105 МПа; h — толщина стенки гибкого колеса под зубьями, мм; р — радиус кривизны срединной поверхности недеформированного гибкого колеса, мм; p=(D + /i)/2; Кю — коэффициент радиальной деформации.
Допускаемый коэффициент запаса по нормальным напряжениям [sa] = 1,5... 1,8.
содержание:
[стр.Введение] [стр.1] [стр.2] [стр.3] [стр.4] [стр.5] [стр.6] [стр.7] [стр.8] [стр.9] [стр.10] [стр.11] [стр.12] [стр.13] [стр.14] [стр.15] [стр.16] [стр.17] [стр.18] [стр.19] [стр.20] [стр.21] [стр.22] [стр.23] [стр.24] [стр.25] [стр.26] [стр.27] [стр.28] [стр.29] [стр.30] [стр.31] [стр.32] [стр.33] [стр.34] [стр.35] [стр.36] [стр.37] [стр.38] [стр.39] [стр.40] [стр.41] [стр.42] [стр.43] [стр.44] [стр.45] [стр.46] [стр.47] [стр.48] [стр.49] [стр.50] [стр.51] [стр.52] [стр.53] [стр.54] [стр.55] [стр.56] [стр.57] [стр.58] [стр.59] [стр.60] [стр.61] [стр.62] [стр.63] [стр.64] [стр.65] [стр.66] [стр.67] [стр.68] [стр.69] [стр.70] [стр.71] [стр.72] [стр.73] [стр.74] [стр.75] [стр.76] [стр.77] [стр.78] [стр.79] [стр.80] [стр.81] [стр.82] [стр.83] [стр.84] [стр.85] [стр.86] [стр.87] [стр.88] [стр.89] [стр.90] [стр.91] [стр.92] [стр.93] [стр.94] [стр.95] [стр.96] [стр.97] [стр.98] [стр.99] [стр.100] [стр.101] [стр.102] [стр.103] [стр.104] [стр.105] [стр.106] [стр.107] [стр.108] [стр.109] [стр.110] [стр.111] [стр.112] [стр.113] [стр.114] [стр.115] [стр.116] [стр.117] [стр.118] [стр.119] [стр.120] [стр.121] [стр.122] [стр.123] [стр.124] [стр.125] [стр.126] [стр.127] [стр.128] [стр.129] [стр.130] [стр.131] [стр.132] [стр.133] [стр.134]
