страница - 9
совпадает с центром тяжести группы болтов, образующих соединение.
Все сложные случаи нагружения соединения можно разделить на ряд простых, которые рассматриваются ниже.
Случай 1 (рис. 3.6). Внешняя сила действует перпендикулярно к плоскости стыка и проходит через его центр тяжести. Болты поставлены с зазором.
Внешняя сила, действующая на каждый болт,
Fa =(3.1)
где z — число болтов.
Случай 2 (рис. 3.7). Внешняя сила действует в плоскости стыка и проходит через его центр тяжести. Болты могут бель поставлены с зазором и без зазора (под развертку).
Внешняя сила, действующая на каждый болт в плоскости стыка,
Ft = FB/г.
Случай 3 (рис. 3.8). Внешний момент Т действует в плоскости стыка. Болты могут быть поставлены с зазором и без зазора.
При прямоугольном стыке (рис. 3.8, а) наиболее нагружен болт, наиболее удаленный от центра тяжести стыка. Действующая на него внешняя сила направлена перпендикулярно к линии, проведенной из центра тяжести стыка к центру болта,
(3.2)
г | |||
+ | |||
+ | и | ||
1 | |||
1 | |||
+ | + | ||
+ | + | ||
Гтах
= 7У,
Рис. 3.8. Схема действия сил в стыке: (3.3) внешний момент действует в плоскости стыка
где rmax — наибольшее расстояние от центра тяжести стыка до центра болта.
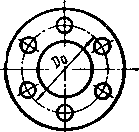
При круглом стыке (рис. 3.8, б) внешняя сила, действующая нз каждый болт в плоскости стыка,
FT = 277(D0z),
где D0 — диаметр окружности, на которой находятся центры болтов.
Случай 4 (рис. 3.9). Внешний момент М действует в плоскости, перпендикулярной к стыку. Болты поставлены с зазором. Наиболее нагружен болт, находящийся дальше других от оси симметрии стыка, относительно которой действует внешний момент. Действующая на него сила направлена по оси болта:
атах — -М/тах/2 it
где /тах — наибольшее расстояние от оси симметрии стыка до оси болта.
Нагружение соединения по рис. 3.10, где внешняя сила наклонена к плоскости стыка и не проходит через его центр тяжести, приводится к случаям 1, 2 и 4. Результирующая внешняя сила, действующая по оси наиболее нагруженного болта, равна алгебраической сумме составляющих от силы Fa и момента М.
Нагружение соединения по рис. 3.11, где в плоскости стыка действует сила Fx и момент Г, приводится к случаям 2 и 3. Ре-
м
Famax rf | T.J | rf | Fqz h rf | rf | \\ rf1 | i | 1 | ||
ЦТ | |||||||||
/ША | V/////M - | /////////, | - - | v//ty////m и | УЖ///, f Fai | V//)// | |||
Рис. 3.9. Схема действия сил в стыке: внешний момент действует в плоскости, перпендикулярной к стыку
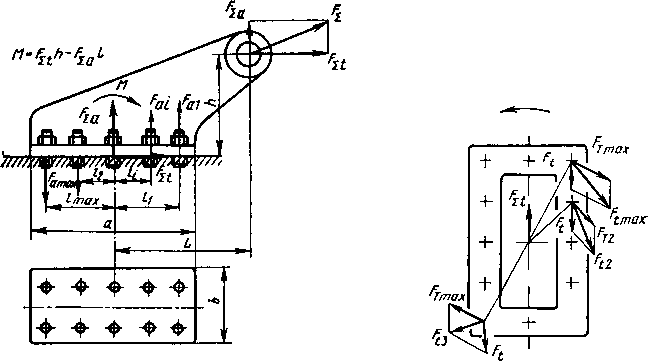
Рис. 3.10. Схема действия сил в стыке:Рис. 3.11. Схема действия
внешняя сила направлена к плоскостисил в стыке: в плоскости
стыка и не проходит через центр тяжестистыка действуют сила и мо-
стыкамент
эультирующая внешняя сила, действующая на наиболее нагруженный болт (fVmax)> равна максимальному значению векторной суммы составляющих от силы F& и момента Т.
3.3. Расчет болтового соединения плит и станин
с фундаментом
При расчете такого соединения помимо определения результирующей внешней силы, действующей на наиболее нагруженный болт, нужно найти усилие затяжки болтов, при котором обеспечивается нераскрытие стыка, и максимальное напряжение смятия фундамента для проверки его прочности.
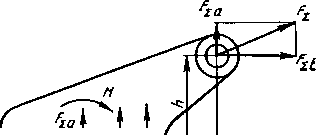
На рис. 3.12 приведены эпюры напряжений в стыке: / — от силы предварительной затяжки Fz3; 2—от силы Fza; 3— от момента
М = Fvh — FzaL; 4, 5, 6 — результирующие эпюры: 4—левый конец стыка «закрыт» (а3 > оРа + ом), 5 — на левом конце стыка результирующее напряжение равно нулю (а3 = о>а + ом, предельно допустимый случай), 6 — левый конец стыка «раскрыт» (а3 < oFa -f- ом).
Расчет принято вести по предельно допустимому случаю (а£л.к = 0):
<*з = oFa + ом\
Оро = F-ZalACi
где Ас — площадь стыка (на рис. 3.12 Ас = ab)\
ifii п*т) ш сщи1к w
ct
где Wc — момент сопротивления стыка изгибу (на рис. 3.12 Wc = baW). Усилие затяжки болта
F3=OaAc/z.
Для проверки прочности «л фундамента определим мак- *м симальное напряжение смятия на правом конце стыка: *
fink
/К /К /К (fs /К
\Т/ Xtr vfr VI/ \/
ф ф- ф-ф
nit! nit ttm
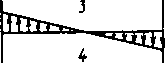
ОГп.к = <*з — Ора +
fink
Рис. 3.12. К расчету фундаментных болтов
содержание:
[стр.Введение] [стр.1] [стр.2] [стр.3] [стр.4] [стр.5] [стр.6] [стр.7] [стр.8] [стр.9] [стр.10] [стр.11] [стр.12] [стр.13] [стр.14] [стр.15] [стр.16] [стр.17] [стр.18] [стр.19] [стр.20] [стр.21] [стр.22] [стр.23] [стр.24] [стр.25] [стр.26] [стр.27] [стр.28] [стр.29] [стр.30] [стр.31] [стр.32] [стр.33] [стр.34] [стр.35] [стр.36] [стр.37] [стр.38] [стр.39] [стр.40] [стр.41] [стр.42] [стр.43] [стр.44] [стр.45] [стр.46] [стр.47] [стр.48] [стр.49] [стр.50] [стр.51] [стр.52] [стр.53] [стр.54] [стр.55] [стр.56] [стр.57] [стр.58] [стр.59] [стр.60] [стр.61] [стр.62] [стр.63] [стр.64] [стр.65] [стр.66] [стр.67] [стр.68] [стр.69] [стр.70] [стр.71] [стр.72] [стр.73] [стр.74] [стр.75] [стр.76] [стр.77] [стр.78] [стр.79] [стр.80] [стр.81] [стр.82] [стр.83] [стр.84] [стр.85] [стр.86] [стр.87] [стр.88] [стр.89] [стр.90] [стр.91] [стр.92] [стр.93] [стр.94] [стр.95] [стр.96] [стр.97] [стр.98] [стр.99] [стр.100] [стр.101] [стр.102] [стр.103] [стр.104] [стр.105] [стр.106] [стр.107] [стр.108] [стр.109] [стр.110] [стр.111] [стр.112] [стр.113] [стр.114] [стр.115] [стр.116] [стр.117] [стр.118] [стр.119] [стр.120] [стр.121] [стр.122] [стр.123] [стр.124] [стр.125] [стр.126] [стр.127] [стр.128] [стр.129] [стр.130] [стр.131] [стр.132] [стр.133] [стр.134]
